Question

【题目】如图，已知∠ABM=37°，AB=20，C是射线BM上一点．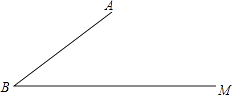

（1）求点A到BM的距离；
（2）在下列条件中，可以唯一确定BC长的是；（填写所有符合条件的序号）
①AC=13；②tan∠ACB= ；③连接AC，△ABC的面积为126．
（3）在（2）的答案中，选择一个作为条件，画出草图，求BC．
（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）

Answer 1

【答案】
（1）

解：作AD⊥BC于D，则∠ADB=90°．

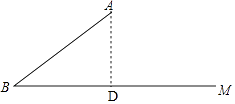
在Rt△ABD中，∵∠ADB=90°，

∴AD=ABsinB=12

（2）②③
（3）

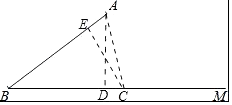
解：方案一：选②，

由（1）得，AD=12，BD=ABcosB=16，

在Rt△ACD中，∵∠ADC=90°，

∴CD= =5，

∴BC=BD+CD=21．

方案二：选③，

作CE⊥AB于E，则∠BEC=90°，

由S△ABC= ABCE得CE=12.6，

在Rt△BEC中，

∵∠BEC=90°，

∴BC= =21

【解析】解： （2）①以点A为圆心、13为半径画圆，与BM有两个交点，不唯一；
②由tan∠ACB= 知∠ACB的大小确定，在△ABC中，∠ACB、∠B及AB确定，此时的三角形唯一；
③AB的长度和三角形的面积均确定，则点C到AC的距离即可确定，则BM上的点C是唯一的；
所以答案是：②③；
【考点精析】解答此题的关键在于理解解直角三角形的相关知识，掌握解直角三角形的依据：①边的关系a2+b2=c2；②角的关系：A+B=90°；③边角关系：三角函数的定义．(注意：尽量避免使用中间数据和除法)．