题目内容
已知:如图,等腰梯形ABCD的边BC在x轴上,点A在y轴的正方向上,A(0,6),D(4,6),且A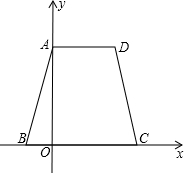 B=2
B=2
.
(1)求点B的坐标;
(2)求经过B、D两点的抛物线y=ax2+bx+6的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,使得S△PBC=
S梯形ABCD?若存在,请求出该点坐标,若不存在,请说明理由.
 B=2
B=2| 10 |
(1)求点B的坐标;
(2)求经过B、D两点的抛物线y=ax2+bx+6的解析式;
(3)在(2)中所求的抛物线上是否存在一点P,使得S△PBC=
| 1 |
| 2 |
(本题满分14分)
(1)在Rt△ABC中,AB=2
,OA=D纵坐标=6,
∴BO=
=2,
∵点B在x轴的负半轴上
∴B(-2,0);
(2)依题意,
得
,
解这个方程组,得
,
∴y=-
x2+2x+6;
(3)∵A(0,6),D(4,6)
∴AD=4
过点D作DE⊥x轴于点E,则四边形DEOA是矩形,
有DE=OA=6,AD=OE=4
∵四边形ABCD是等腰梯形
∴CD=AB=2
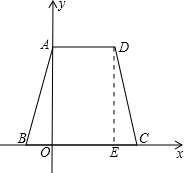
由勾定理得:CE=
=
=2
∴OC=2+4=6
∴C(6,0)
∵B(-2,0)
∴BC=8
∴S梯形ABCD=
×(4+8)*6=36
∵S△PBC=
S梯形ABCD
∴S△PBC=
*36=18
设点P的坐标为(x,y),则△PBC的BC边上的高为|y|
∴
×8×|y|=18
∴y=±
∴p1(x,
),p2(x,-
)
∵点p1(x,-
)在抛物线上
∴-
x2+2x+6=-
解这个方程得:x1=-3,x2=7
点P1的坐标为(-3,-
),(7,-
)
同理可求得:P2的坐标为(2+
,
),(2-
,
)
所P点坐标为(-3,-
),(7,-
),(2+
,
),(2-
,
).
(1)在Rt△ABC中,AB=2
| 10 |
∴BO=
| AB2-AO2 |
∵点B在x轴的负半轴上
∴B(-2,0);
(2)依题意,
得
|
解这个方程组,得
|
∴y=-
| 1 |
| 2 |
(3)∵A(0,6),D(4,6)
∴AD=4
过点D作DE⊥x轴于点E,则四边形DEOA是矩形,
有DE=OA=6,AD=OE=4
∵四边形ABCD是等腰梯形
∴CD=AB=2
| 10 |

由勾定理得:CE=
| DC2-CE2 |
(2
|
∴OC=2+4=6
∴C(6,0)
∵B(-2,0)
∴BC=8
∴S梯形ABCD=
| 1 |
| 2 |
∵S△PBC=
| 1 |
| 2 |
∴S△PBC=
| 1 |
| 2 |
设点P的坐标为(x,y),则△PBC的BC边上的高为|y|
∴
| 1 |
| 2 |
∴y=±
| 9 |
| 2 |
∴p1(x,
| 9 |
| 2 |
| 9 |
| 2 |
∵点p1(x,-
| 9 |
| 2 |
∴-
| 1 |
| 2 |
| 9 |
| 2 |
解这个方程得:x1=-3,x2=7
点P1的坐标为(-3,-
| 9 |
| 2 |
| 9 |
| 2 |
同理可求得:P2的坐标为(2+
| 7 |
| 9 |
| 2 |
| 7 |
| 9 |
| 2 |
所P点坐标为(-3,-
| 9 |
| 2 |
| 9 |
| 2 |
| 7 |
| 9 |
| 2 |
| 7 |
| 9 |
| 2 |

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
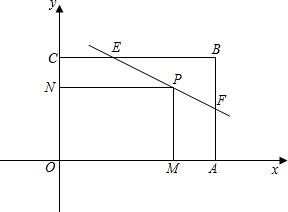 线EF交边BC于E,且sin∠BEF=
线EF交边BC于E,且sin∠BEF=
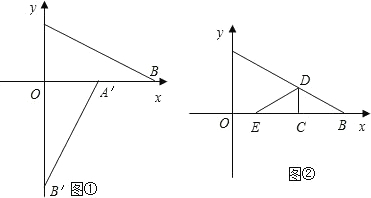 若不存在,请说明理由.
若不存在,请说明理由.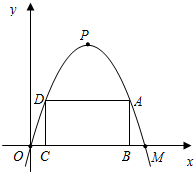
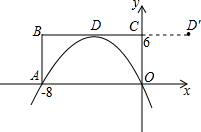 过A、D两点,如图所示.
过A、D两点,如图所示.