题目内容
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=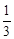 ,AD=1.
,AD=1.
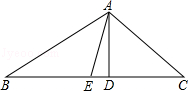
(1)求BC的长;
(2)求tan∠DAE的值.
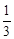 ,AD=1.
,AD=1.
(1)求BC的长;
(2)求tan∠DAE的值.
(1)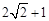 。
。
(2)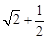
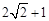 。
。(2)
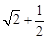
分析:(1)先由三角形的高的定义得出∠ADB=∠ADC=90°,再解Rt△ADC,得出DC=1;解Rt△ADB,得出AB=3,根据勾股定理求出BD=
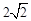 ,然后根据BC=BD+DC即可求解。
,然后根据BC=BD+DC即可求解。(2)先由三角形的中线的定义求出CE的值,则DE=CE﹣CD,然后在Rt△ADE中根据正切函数的定义即可求解。
解:(1)在△ABC中,∵AD是BC边上的高,∴∠ADB=∠ADC=90°。
在△ADC中,∵∠ADC=90°,∠C=45°,AD=1,∴DC=AD=1。
在△ADB中,∵∠ADB=90°,sinB=
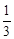 ,AD=1,
,AD=1,∴
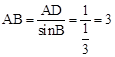 。
。∴
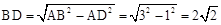 。
。∴
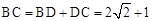 。
。(2)∵AE是BC边上的中线,∴CE=
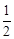 BC=
BC=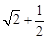 。
。∴DE=CE﹣CD=
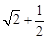 。
。∴
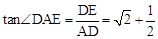 。
。
练习册系列答案
相关题目
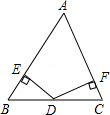
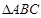 中,
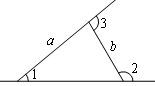
中,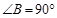 ,若按图中虚线剪去
,若按图中虚线剪去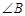 ,则
,则 等于( )
等于( )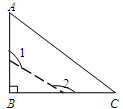
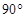
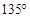
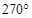
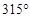
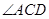 的平分线交BA延长线于点E,
的平分线交BA延长线于点E,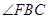 的平分线交AC延长线于点G.若CE =" BC" = BG,则
的平分线交AC延长线于点G.若CE =" BC" = BG,则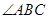 的度数 度.
的度数 度.
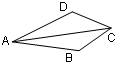
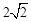 ,BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为 .
,BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为 .