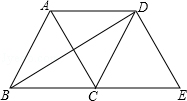
题目内容
在△ABC中,AB=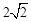 ,BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为 .
,BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为 .
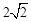 ,BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为 .
,BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为 .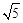 或
或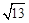 。
。分两种情况:如图,
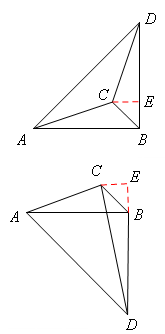
当点D与C在AB同侧,BD=AB=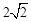 ,
,
过点C作CE⊥BD于点E,则
∵BC=1,∠ABC=450,∴CE=BE=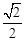 。∴ED=
。∴ED=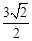 。
。
在Rt△CDE中,由勾股定理CD=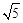 。
。
当点D与C在AB异侧,BD=AB=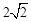 ,
,
过点C作CE⊥BC交DB的延长线于点E,则
∵BC=1,∠BCE=450,∴CE=BE=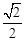 。∴ED=
。∴ED=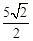 。
。
在Rt△CDE中,由勾股定理CD=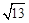 。
。
综上所述,线段CD的长为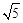 或
或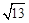 。
。

当点D与C在AB同侧,BD=AB=
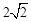 ,
,过点C作CE⊥BD于点E,则
∵BC=1,∠ABC=450,∴CE=BE=
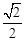 。∴ED=
。∴ED=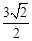 。
。在Rt△CDE中,由勾股定理CD=
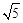 。
。当点D与C在AB异侧,BD=AB=
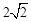 ,
,过点C作CE⊥BC交DB的延长线于点E,则
∵BC=1,∠BCE=450,∴CE=BE=
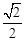 。∴ED=
。∴ED=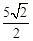 。
。在Rt△CDE中,由勾股定理CD=
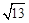 。
。综上所述,线段CD的长为
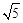 或
或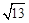 。
。
练习册系列答案
相关题目
 、B
、B 、B
、B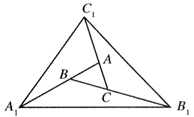
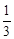 ,AD=1.
,AD=1.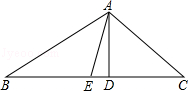
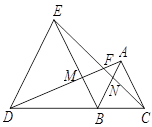
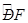 的中点.
的中点.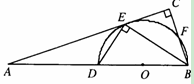
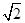 ,求BC的长.
,求BC的长.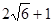 和
和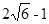 ,则斜边长为 .
,则斜边长为 .