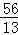题目内容
在Rt△ABC中,∠ACB=90°,tan∠BAC=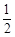 . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.

(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设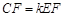 ,则k = ;
,则k = ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
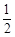 . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设
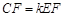 ,则k = ;
,则k = ;(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
(1)k=1(2)证明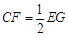 ,则可得
,则可得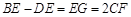 . (3)当点D在靠近点C的
. (3)当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为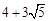
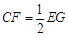 ,则可得
,则可得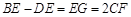 . (3)当点D在靠近点C的
. (3)当点D在靠近点C的三等分点时,线段CF的长度取得最大值为
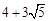
试题分析:解:(1)k=1; .
(2)如图2,过点C作CE的垂线交BD于点G,设BD与AC的交点为Q.
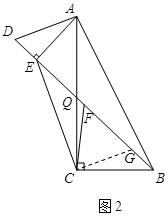
由题意,tan∠BAC=
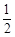 ,
,∴
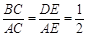 .
.∵D、E、B三点共线,
∴AE⊥DB.
∵∠BQC=∠AQD,∠ACB=90°,
∴∠QBC=∠EAQ.
∵∠ECA+∠ACG=90°,∠BCG+∠ACG=90°,
∴∠ECA=∠BCG.
∴
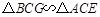 .
.∴
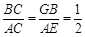 .
.∴GB=DE.
∵F是BD中点,
∴F是EG中点.
在
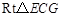 中,
中,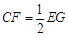 ,
,∴
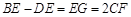 . . .
. . . (3)情况1:如图,当AD=
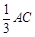 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,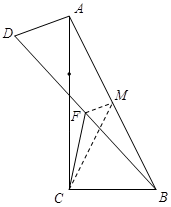
∵∠ACB=90°, tan∠BAC=
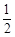 ,且BC= 6,
,且BC= 6,∴AC=12,AB=
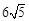 .
.∵M为AB中点,∴CM=
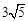 ,
,∵AD=
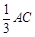 ,
,∴AD=
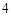 .
.∵M为AB中点,F为BD中点,
∴FM=
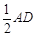 = 2.
= 2.∴当且仅当M、F、C三点共线且M在线段CF上时CF最大,此时CF=CM+FM=
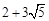 .
.情况2:如图,当AD=
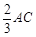 时,取AB的中点M,连结MF和CM,
时,取AB的中点M,连结MF和CM,
类似于情况1,可知CF的最大值为
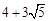 .
. . 6分
综合情况1与情况2,可知当点D在靠近点C的
三等分点时,线段CF的长度取得最大值为
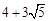
点评:本题难度较大。主要考查学生对综合型几何题的掌握与灵活运用。这类题型需要学生多培养数形结合思想,多做训练来提高题感和反应能力,为中考常考题型,要牢固掌握。

练习册系列答案
相关题目

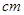 ,这两地的实际距离是
,这两地的实际距离是  .
.
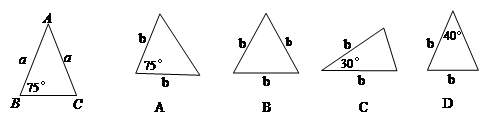
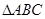 中,AB=AC=10cm, BC=16cm,DE=4cm.线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动.过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0).
中,AB=AC=10cm, BC=16cm,DE=4cm.线段DE(端点D从点B开始)沿BC边以1cm/s的速度向点C运动,当端点E到达点C时停止运动.过点E作EF∥AC交AB于点F,连接DF,设运动的时间为t秒(t≥0).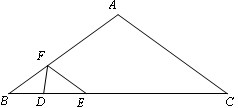
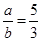 ,则
,则 .
.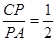 ,PB=2,求BC的长.
,PB=2,求BC的长.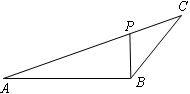
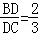 ,
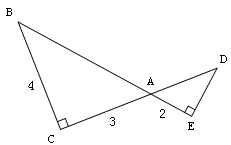
, ,AD、BE交于F,则
,AD、BE交于F,则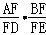 的值是( )
的值是( )
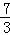 B.
B.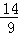 C.
C.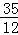 D.
D.