题目内容
【题目】如图，在Rt△ABC中，∠ACB=90°，BC，AC，AB边的中点分别是点D，E，F，则下列说法可能不正确的为（ ）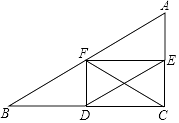
A.四边形CDFE是矩形
B.DE=CF= 
AB
C.S△ABC=4S△AEF
D.∠B=30°
【答案】D
【解析】解：∵点D，E，F分别是BC，AC，AB的中点，
∴DF∥AC，EF∥BC，
∴四边形CDFE是平行四边形，
∵∠ACB=90°，
∴平行四边形CDFE是矩形，故A正确，
∴CF=DE，
∵点D，E是BC，AC中点，
∴DE= 
AB，
∴DE=CF= AB，
故B正确，
∵点E，F是AC，AB的中点，
∴EF= BC，EF∥BC，
∴△AEF∽△ACB，
∴ 
=（ 
）2= 
，
∴S△ABC=4S△AEF，
故C正确，
所以，A，B，C都正确，
即：不正确的只有D，
所以答案是：D．
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识，掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半，以及对矩形的判定方法的理解，了解有一个角是直角的平行四边形叫做矩形；有三个角是直角的四边形是矩形；两条对角线相等的平行四边形是矩形．
阅读快车系列答案【题目】在某次试验中，测得两个变量m和v之间的4组对应数据如下表：
m | 1 | 2 | 3 | 4 |
v | 0.01 | 2.9 | 8.03 | 15.1 |
则m与v之间的关系最接近于下列各关系式中的( )
A. v＝2m－1B. v＝m2－1C. v＝3m－3D. v＝m＋1
【题目】为了贯彻落实市委政府提出的“精准扶贫”精神，某校特制定了一系列帮扶A、B两贫困村的计划，现决定从某地运送152箱鱼苗到A、B两村养殖，若用大小货车共15辆，则恰好能一次性运完这批鱼苗，已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆，其运往A、B两村的运费如表：
车型 | 目的地 | ||
A村（元/辆） | B村（元/辆） | ||
大货车 | |||
800 | 900 | ||
小货车 | 400 | 600 | |
（1）求这15辆车中大小货车各多少辆？
（2）现安排其中10辆货车前往A村，其余货车前往B村，设前往A村的大货车为x辆，前往A、B两村总费用为y元，试求出y与x的函数解析式．
（3）在（2）的条件下，若运往A村的鱼苗不少于100箱，请你写出使总费用最少的货车调配方案，并求出最少费用．
