题目内容
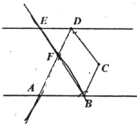
【题目】如图,已知![]() 为两条相互平行的直线
为两条相互平行的直线![]() ,
,![]() 之间一点,
之间一点,![]() 和
和![]() 的角平分线相交于
的角平分线相交于![]() ,
,![]() .
.

(1)求证:![]() ;
;
(2)连结![]() 当
当![]() 且
且![]() 时,求
时,求![]() 的度数;
的度数;
(3)若![]() 时,将线段
时,将线段![]() 沿直线
沿直线 ![]() 方向平移,记平移后的线段为
方向平移,记平移后的线段为![]() (
(![]() ,
,![]() 分别对应
分别对应![]() 、
、![]() 当
当![]() 时,请直接写出
时,请直接写出![]() 的度数_______.
的度数_______.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据平行线的性质得到∠EDF=∠DAB,根据角平分线 的定义得到∠EDF=∠ADC,根据平行线的判定定理即可得到结论;
(2)设∠DCF=α,则∠CFB=1.5α,根据平行线的性质得到∠ABF=∠CFB=1.5α,根据角平分线的定义得到∠ABC=2∠ABF=3α,根据平行线的性质即可得到结论;
(3)根据已知条件得到四边形BCDF是平行四边形,得到∠CDF=∠CBF,根据角平分线的定义得到∠ABC=2∠CBF,∠CDE=2∠CDF,求得∠DCB=120°,根据平行的性质得到BC∥PQ,根据四边形的内角和列方程即可得到结论.
(1)∵AB∥DE,
∴∠EDF=∠DAB,
∵DF平分∠EDC,
∴∠EDF=∠ADC,
∴∠ADC=∠DAB,
∵∠FDC+∠ABC=180°,
∴∠DAB+∠ABC=180°,
∴AD∥BC;
(2)∵∠CFB=![]() ∠DCF,
∠DCF,
∴设∠DCF=α,则∠CFB=1.5α,
∵CF∥AB,
∴∠ABF=∠CFB=1.5α,
∵BE平分∠ABC,
∴∠ABC=2∠ABF=3α,
∵AD∥BC,
∴∠ADC+∠BCD=180°,
∵∠FDC+∠ABC=180°,
∴∠BCD=∠ABC=3α,
∴∠BCF=2α,
∵CF∥AB,
∴∠ABC+∠BCF=180°,
∴3α+2α=180°,
∴α=36°,
∴∠BCD=3×36°=108°;
(3)如图,

∵∠DCF=∠CFB,
∴BF∥CD,
∵AD∥BC,
∴四边形BCDF是平行四边形,
∴∠CDF=∠CBF,
∵AD,BE分别平分∠ABC,∠CDE,
∴∠ABC=2∠CBF,∠CDE=2∠CDF,
∴∠ABC=2∠CDF,
∵∠FDC+∠ABC=180°,
∴∠ABC=120°,∠CDF=60°,
∴∠DCB=120°,
∴∠ABC=120°,
∴∠DAB=60°,
∵线段BC沿直线AB方向平移得到线段PQ,
∴BC∥PQ,
∴∠APQ=120°,
∵∠PQD-∠QDC=20°,
∴∠QDC=∠PQD-20°,
∴∠FDC+∠CDQ+∠PQD+∠APQ+∠DAB=60°+∠PQD-20°+∠PQD+120°+60°=360°,
∴∠PQD=70°.
故答案为:70°.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案