题目内容
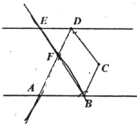
【题目】如图,四边形ABCD为矩形,F为对角线BD上一点,点E在BA延长线上.
(1)如图①,若F为矩形对角线AC、BD的交点,点E在BA延长线上且BE=AC,连接DE,M是DE的中点,连接BM,FM若AD=6,FM=![]() ,求线段AE的长;
,求线段AE的长;
(2)如图②,过点F作FE⊥BD交AD于点H,交BA延长线于点E,连接AF,当FD=FE时,求证:HA+AB=![]() AF.
AF.

【答案】(1)3;(2)见解析
【解析】
(1)由矩形的性质可得AC=BD,BF=DF,由中位线定理可得BE=2MF,再由勾股定理可求AB的长,即可求AE的长;
(2)如图②,过点F作FN⊥AF交AB的延长线于点N,由“ASA”可证△EFN≌△DFA,可得∠DAF=∠N,AF=FN,由等腰直角三角形的性质可得AN=![]() ,由“ASA”可证△AHF≌△NBF,可证AH=BN,即可得结论.
,由“ASA”可证△AHF≌△NBF,可证AH=BN,即可得结论.
(1)∵四边形ABCD是矩形
∴AC=BD,BF=DF,
∵M是DE的中点,BF=DF,
∴BE=2MF=![]() ,
,
∵BE=AC,AC=BD
∴BD=![]() ,
,
∴AB=![]() ,
,
∴AE=BE﹣AB=3,
(2)如图②,过点F作FN⊥AF交AB的延长线于点N,

∵EF⊥DF,EA⊥AD,
∴∠E+∠AHE=90°,∠ADF+∠DHF=90°,
∴∠E=∠ADF,
∵∠AFN=∠EFD=90°,
∴∠AFD=∠EFN,且∠E=∠ADF,且EF=DF,
∴△EFN≌△DFA(ASA)
∴∠DAF=∠N,AF=FN,且∠AFN=90°,
∴AN=![]() AF,
AF,
∵∠AFN=∠EFB=90°,
∴∠AFH=∠BFN,且∠DAF=∠N,AF=FN,
∴△AHF≌△NBF(ASA),
∴AH=BN(全等三角形对应边相等),
∵AN=![]() AF,
AF,
∴AB+BN=AB+AH=![]() AF,
AF,

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目