题目内容
【题目】在![]() 中,
中,![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,射线
,射线![]() 与射线
与射线![]() 相交于点
相交于点![]() ,若
,若![]() 是等腰三角形,则
是等腰三角形,则![]() 的度数为__________.
的度数为__________.
【答案】![]() 或36°或
或36°或![]()
【解析】
分三种情形:①当B′E=B′A时,如图1所示.②当EB′=AE时,如图2所示.③如图3中,当B′A=B′E时,分别构建方程求解即可.
解:①当B′E=B′A时,如图1所示:
∵AB=AC,
∴∠B=∠BCA,
由折叠得:∠B=∠B′,∠BCA=∠B′CA,
设∠B=x,则∠B′=∠BCA=∠B′CA=x,
∴∠B′AE=∠B′EA=3x,
在△AEB′中,由内角和定理得:
3x+3x+x=180°,
∴x=![]() ,即:∠B=
,即:∠B=![]() .
.
②当EB′=AE时,如图2所示: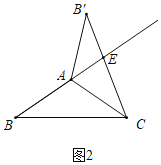
∵AB=AC,
∴∠B=∠BCA,
由折叠得:∠B=∠B′,∠BCA=∠B′CA,
设∠B=x,则∠B′=∠BCA=∠B′CA=x,∠AEB′=3x,
在△AEB′中,由内角和定理得:x+x+3x=180°,
∴x=36°,即∠B=36°.
③如图3中,当B′A=B′E时,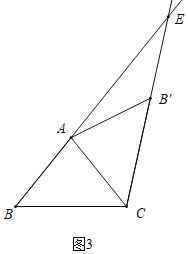
∵AB=AC,
∴∠B=∠BCA,
由折叠得:∠B=∠AB′C,∠BCA=∠B′CA,
设∠B=x,则∠B′=∠BCA=∠B′CA=x,∠AEB′=![]() x,∠EAC=2x,
x,∠EAC=2x,
在△AEC中,由内角和定理得:x+2x+![]() x=180°,
x=180°,
∴x=![]() ,即∠B=
,即∠B=![]() .
.
综上所述,满足条件的∠B的度数为![]() 或36°或
或36°或![]() .
.
故答案为![]() 或36°或
或36°或![]() .
.

练习册系列答案
相关题目