ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΓΕ¥ζ ΐ―ßΓΖ÷–Φ«‘ΊΘ§–Έ»γx2+8xΘΫ33ΒΡΖΫ≥ΧΘ§«σ’ΐ ΐΫβΒΡΦΗΚΈΖΫΖ® «ΘΚΓΑ»γΆΦ1Θ§œ»ΙΙ‘λ“ΜΗωΟφΜΐΈΣx2ΒΡ’ΐΖΫ–ΈΘ§‘Ό“‘’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ“Μ±ΏœρΆβΙΙ‘λΥΡΗωΟφΜΐΈΣ2xΒΡΨΊ–ΈΘ§ΒΟΒΫ¥σ’ΐΖΫ–ΈΒΡΟφΜΐΈΣ33+16ΘΫ49Θ§‘ρΗΟΖΫ≥ΧΒΡ’ΐ ΐΫβΈΣ7©¹4ΘΫ3Θ°Γ±–Γ¥œΑ¥¥ΥΖΫΖ®ΫβΙΊ”ΎxΒΡΖΫ≥Χx2+10x+mΘΫ0 ±Θ§ΙΙ‘λ≥ω»γΆΦ2Υυ ΨΒΡΆΦ–ΈΘ§“―÷Σ“θ”Α≤ΩΖ÷ΒΡΟφΜΐΈΣ50Θ§‘ρΗΟΖΫ≥ΧΒΡ’ΐ ΐΫβΈΣΘ®ΓΓΓΓΘ©


A.6B.![]() C.
C.![]() D.
D.![]()
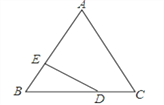
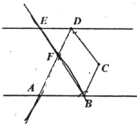
ΓΨ¥πΑΗΓΩD
ΓΨΫβΈωΓΩ
ΗυΨί“―÷ΣΒΡ ΐ―ßΡΘ–ΆΘ§Ά§άμΩ…ΒΟΩ’ΑΉ–Γ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ![]() Θ§œ»ΦΤΥψ≥ω¥σ’ΐΖΫ–ΈΒΡΟφΜΐ
Θ§œ»ΦΤΥψ≥ω¥σ’ΐΖΫ–ΈΒΡΟφΜΐ![]() “θ”Α≤ΩΖ÷ΒΡΟφΜΐ+4Ηω–Γ’ΐΖΫ–ΈΒΡΟφΜΐΘ§Ω…ΒΟ¥σ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΘ§¥”ΕχΒΟΫα¬έΘ°
“θ”Α≤ΩΖ÷ΒΡΟφΜΐ+4Ηω–Γ’ΐΖΫ–ΈΒΡΟφΜΐΘ§Ω…ΒΟ¥σ’ΐΖΫ–ΈΒΡ±Ώ≥ΛΘ§¥”ΕχΒΟΫα¬έΘ°
ΫβΘΚ»γΆΦ2Θ§œ»ΙΙ‘λ“ΜΗωΟφΜΐΈΣx2ΒΡ’ΐΖΫ–ΈΘ§‘Ό“‘’ΐΖΫ–ΈΒΡ±Ώ≥ΛΈΣ“Μ±ΏœρΆβΙΙ‘λΥΡΗωΟφΜΐΈΣ![]() ΒΡΨΊ–ΈΘ§ΒΟΒΫ¥σ’ΐΖΫ–ΈΒΡΟφΜΐΈΣ
ΒΡΨΊ–ΈΘ§ΒΟΒΫ¥σ’ΐΖΫ–ΈΒΡΟφΜΐΈΣ![]() Θ§‘ρΗΟΖΫ≥ΧΒΡ’ΐ ΐΫβΈΣ
Θ§‘ρΗΟΖΫ≥ΧΒΡ’ΐ ΐΫβΈΣ![]() Θ°
Θ°
Ι ―ΓΘΚDΘ°

ΓΨΧβΡΩΓΩΡ≥’ΰΗ°≤ΩΟ≈Ϋχ––ΙΪΈώ‘±’–ΤΗΩΦ ‘Θ§Τδ÷–»ΐ»Υ÷–¬Φ»Γ“Μ»ΥΘ§ΥϊΟ«ΒΡ≥…Φ®»γœ¬ΘΚ
»Υ | ≤β ‘≥…Φ® | ||
ΧβΡΩ | ΦΉ | ““ | ±ϊ |
ΈΡΜ·ΩΈ÷Σ Ε | 74 | 87 | 69 |
Οφ ‘ | 58 | 74 | 70 |
ΤΫ ±±μœ÷ | 87 | 43 | 65 |
Θ®1Θ©Α¥’’ΤΫΨυ≥…Φ®ΦΉΓΔ““ΓΔ±ϊΥ≠”Π±Μ¬Φ»ΓΘΩ
Θ®2Θ©»τΑ¥’’ΈΡΜ·ΩΈ÷Σ ΕΓΔΟφ ‘ΓΔΤΫ ±±μœ÷ΒΡ≥…Φ®“―4ΘΚ3ΘΚ1ΒΡ±»άΐ¬Φ»ΓΘ§ΦΉΓΔ““ΓΔ±ϊΥ≠”Π±Μ¬Φ»ΓΘΩ