Question

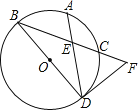
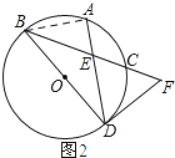
【题目】（本题满分10分）如图，BD是⊙O的直径，点A是劣弧BC的中点，DF是⊙O的切线交BC于点F，AD交BC于点E．

（1）求证：EF=DF；

（2）若AE=2，ED=4，求EF的长．

Answer 1

【答案】见解析

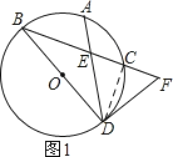
【解析】解：（1）如图1所示：连接CD．

∵点A是劣弧BC的中点，

∴弧长AB=弧长AC．

∴∠ADB=∠ADC．

∵BD是圆O的直径，

∴∠DCB=90°．

∴∠CED+∠EDC=90°．

∵DF是圆O的切线，

∴∠BDF=90°．

∴∠EDF+∠BDE=90°．

∴∠FED=∠EDF．

∴EF=DF．

（2）如图2所示：连接AB．

∵点A是劣弧BC的中点，

∴弧长AB=弧长AC．

∴∠ADB=∠ABC．

又∵∠A=∠A，

∴△ABE∽△ADB．

∴AB2=AEAD．

∴AB=2．

∵BD是圆O的直径，

∴∠DAB=90°．

∴tan∠BDA=tan∠ABC=．

∴∠BDA=∠ABC=30°．

∴BD=2AB=4，∠DBF=30°．

∴EF=DF=DB×=4．