题目内容
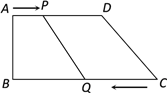
【题目】如图,在直角梯形ABCD中,AD∥BC,∠B = 90,AD = 24厘米,AB = 8厘米,BC = 30厘米,动点P从A开始沿AD边向D以每秒1厘米的速度运动,动点Q从点C开始沿CB边向B以每秒3厘米的速度运动,P,Q分别从点A、C同时出发,当其中一点到达端点时, 另一点也随之停止运动.
设运动时间为t秒.
(1) 当t在什么时间范围时,CQ>PD?
(2) 存在某一时刻t,使四边形APQB是正
方形吗?若存在,求出t值,若不存在,请说明理由.
【答案】(1)6<t≤10;(2)不存在,理由见解析
【解析】试题分析:(1)根据CQ>PD建立关于t的不等式即可求出t的取值范围;
(2)通过反证法,即令AP 和BQ 都等于AB,而建立起来的两个关于t的方程却无解,即可得出结论.
解:(1) ∵ CQ = 3×t,PD = 24-1×t.
∴ 由CQ>PD有3×t>24-1×t,解得t>6.
又因为P、Q点运动的时间最多只能是30÷3 = 10 (秒).
∴ 6<t≤10, 即当6<t≤10时CQ>PD.
(2) 若四边形是正方形,则AP = AB且BQ = AB,
∴ 1×t = 8 且 30-3×t = 8,显然t无解.
即不存在t值使得四边形是正方形

练习册系列答案
相关题目