题目内容
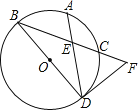
【题目】如图,二次函数y=ax2+bx+c（a≠0）的图象经过点（1,2）且与x轴交点的横坐标分别为x1，x2，其中﹣1＜x1＜0.1＜x2＜2.下列结论：4a+2b+c＜0；2a+b＜0；b2+8a＞4ac；
a＜﹣1；其中结论正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】由抛物线的开口向下知a<0，
与y轴的交点为在y轴的正半轴上，得c>0，
对称轴为x=
<1，∵a<0，∴2a+b<0，
而抛物线与x轴有两个交点,∴
4ac>0，
当x=2时，y=4a+2b+c<0，当x=1时，a+b+c=2.
∵
>2，∴4ac
<8a，∴
+8a>4ac，
∵①a+b+c=2，则2a+2b+2c=4，②4a+2b+c<0，③ab+c<0.
由①，③得到2a+2c<2，由①，②得到2ac<4，4a2c<8，
上面两个相加得到6a<6，∴a<1.故选D.
练习册系列答案
津桥教育计算小状元系列答案
相关题目
【题目】某校举办八年级学生数学素养大赛，比赛共设四个项目：七巧板拼图，趣题巧解，数学应用，魔方复原，每个项目得分都按一定百分比折算后记入总分，下表为甲，乙，丙三位同学得分情况（单位：分）
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
（1）比赛后，甲猜测七巧板拼图，趣题巧解，数学应用，魔方复原这四个项目得分分别按10%，40%，20%，30%折算△记入总分，根据猜测，求出甲的总分；
（2）本次大赛组委会最后决定，总分为80分以上（包含80分）的学生获一等奖，现获悉乙，丙的总分分别是70分，80分．甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分，问甲能否获得这次比赛的一等奖？
