题目内容
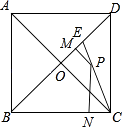
【题目】如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角,使其由45°改为30°. 已知原传送带AB长为4米.
(1)求新传送带AC的长度;
(2)如果需要在货物着地点C的左侧留出2米的通道,试判断距离B点4米的货物![]() 是否需要挪走,并说明理由.
是否需要挪走,并说明理由.

【答案】(1)5.6m;(2)应挪走.
【解析】试题解析:试题分析:(1)在构建的直角三角形中,首先求出两个直角三角形的公共直角边,进而在Rt△ACD中,求出AC的长.
(2)通过解直角三角形,可求出BD、CD的长,进而可求出BC、PC的长.然后判断PC的值是否大于2米即可.
试题解析:(1)如图,
在Rt△ABD中,AD=ABsin45°=4![]() .
.
在Rt△ACD中,
∵∠ACD=30°,
∴AC=2AD=8.
即新传送带AC的长度约为8米;
(2)结论:货物MNQP不用挪走.
解:在Rt△ABD中,BD=ABcos45°=4![]() =4.
=4.
在Rt△ACD中,CD=![]() AD=4
AD=4![]() .
.
∴CB=CD-BD=4![]() -4≈2.8.
-4≈2.8.
∵PC=PB-CB≈5-2.8=2.2>2,
∴货物MNQP不应挪走.

 云南师大附小一线名师提优作业系列答案
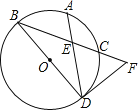
云南师大附小一线名师提优作业系列答案【题目】如图,二次函数![]() 的图像交
的图像交![]() 轴于
轴于![]() ,交
,交![]() 轴于点
轴于点![]() ,连接直线
,连接直线![]() .
.
(1)求二次函数的解析式;
(2)点![]() 在二次函数的图像上,圆
在二次函数的图像上,圆![]() 与直线
与直线![]() 相切,切点为
相切,切点为![]() .
.
①若![]() 在
在![]() 轴的左侧,且△
轴的左侧,且△![]() ∽△
∽△![]() ,求点
,求点![]() 的坐标;
的坐标;
②若圆![]() 的半径为4,求点
的半径为4,求点![]() 的坐标.
的坐标.
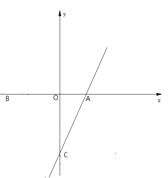
【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有 个,分别为 ;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.