题目内容
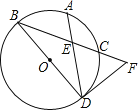
【题目】如图,正方形ABCD中,点E,F分别在边AB,BC上,AF=DE,AF和DE相交于点G.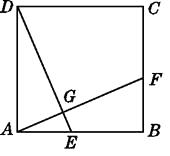
(1)观察图形,写出图中所有与∠AED相等的角;
(2)选择图中与∠AED相等的任意一个角,并加以证明.
【答案】
(1)解:由题图可知,∠DAG,∠AFB,∠CDE与∠AED相等 .
(2)解:(答案不唯一)选择∠DAG=∠AED,证明如下:
由正方形ABCD得
∠DAB=∠B=90°,AD=AB.
在Rt△DAE与Rt△ABF中,![]()
∴Rt△DAE≌Rt△ABF(HL).
∴∠ADE=∠BAF.
∵∠DAG+∠BAF=90°,∠ADE+∠AED=90°,
∴∠DAG=∠AED
【解析】(1)根据正方形的性质可以得出∠DAB=∠B=90°,AD=AB,然后利用HL判断出Rt△DAE≌Rt△ABF,根据全等三角形对应角相等得出∠ADE=∠BAF ,∠DEA=∠AFB ,然后根据等角的余角相等得出∠DAG=∠AED ,根据同角的余角相等得出∠CDG=∠DAG,从而利用等量代换得出∠CDG=∠AED ;
(2)此题是一道开放性的命题,一般选择自己十拿九稳的结论进行证明:根据正方形的性质可以得出∠DAB=∠B=90°,AD=AB,然后利用HL判断出Rt△DAE≌Rt△ABF,根据全等三角形对应角相等得出∠ADE=∠BAF ,,然后根据等角的余角相等得出∠DAG=∠AED 。

 名校课堂系列答案
名校课堂系列答案【题目】佳佳向探究一元三次方程x3+2x2﹣x﹣2=0的解的情况,根据以往的学习经验,他想到了方程与函数的关系,一次函数y=kx+b(k≠0)的图象与x轴交点的横坐标即为一元一次方程kx+b(k≠0)的解,二次函数y=ax2+bx+c(a≠0)的图象与x轴交点的横坐标即为一元二次方程ax2+bx+c=0(a≠0)的解,如:二次函数y=x2﹣2x﹣3的图象与x轴的交点为(﹣1,0)和(3,0),交点的横坐标﹣1和3即为x2﹣2x﹣3=0的解.
根据以上方程与函数的关系,如果我们直到函数y=x3+2x2﹣x﹣2的图象与x轴交点的横坐标,即可知方程x3+2x2﹣x﹣2=0的解.
佳佳为了解函数y=x3+2x2﹣x﹣2的图象,通过描点法画出函数的图象.
x | … | ﹣3 | ﹣ | ﹣2 | ﹣ | ﹣1 | ﹣ | 0 |
| 1 |
| 2 | … |
y | … | ﹣8 | ﹣ | 0 |
| m | ﹣ | ﹣2 | ﹣ | 0 |
| 12 | … |
(1)直接写出m的值,并画出函数图象;
(2)根据表格和图象可知,方程的解有 个,分别为 ;
(3)借助函数的图象,直接写出不等式x3+2x2>x+2的解集.

【题目】某校举办八年级学生数学素养大赛,比赛共设四个项目:七巧板拼图,趣题巧解,数学应用,魔方复原,每个项目得分都按一定百分比折算后记入总分,下表为甲,乙,丙三位同学得分情况(单位:分)
七巧板拼图 | 趣题巧解 | 数学应用 | 魔方复原 | |
甲 | 66 | 89 | 86 | 68 |
乙 | 66 | 60 | 80 | 68 |
丙 | 66 | 80 | 90 | 68 |
(1)比赛后,甲猜测七巧板拼图,趣题巧解,数学应用,魔方复原这四个项目得分分别按10%,40%,20%,30%折算△记入总分,根据猜测,求出甲的总分;
(2)本次大赛组委会最后决定,总分为80分以上(包含80分)的学生获一等奖,现获悉乙,丙的总分分别是70分,80分.甲的七巧板拼图、魔方复原两项得分折算后的分数和是20分,问甲能否获得这次比赛的一等奖?