题目内容
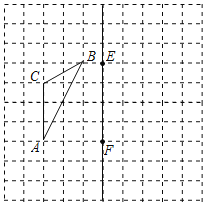
【题目】已知如图,在正方形![]() 中,
中,![]() 为
为![]() 的中点,
的中点,![]() ,
,![]() 平分
平分![]() 并交
并交![]() 于
于![]() .求证:
.求证:![]()

【答案】见解析
【解析】
取DA的中点F,连接FM,根据正方形的性质可得DA=AB,∠A=∠ABC=∠CBE=90°,然后利用ASA即可证出△DFM≌△MBN,再根据全等三角形的性质即可得出结论.
解:取DA的中点F,连接FM

∵四边形![]() 是正方形
是正方形
∴DA=AB,∠A=∠ABC=∠CBE=90°
∴∠FDM+∠AMD=90°
∵![]()
∴∠BMN+∠AMD=90°
∴∠FDM=∠BMN
∵点F、M分别是DA、AB的中点
∴DF=FA=![]() DA=
DA=![]() AB=AM=MB
AB=AM=MB
∴△AFM为等腰直角三角形
∴∠AFM=45°
∴∠DFM=180°-∠AFM=135°
∵![]() 平分
平分![]()
∴∠CBN=![]() =45°
=45°
∴∠MBN=∠ABC+∠CBN=135°
∴∠DFM=∠MBN
在△DFM和△MBN中

∴△DFM≌△MBN
∴![]()

练习册系列答案
相关题目