题目内容
【题目】已知某服装厂现有![]() 种布料70米,
种布料70米,![]() 种布料52米,现计划用这两种布料生产
种布料52米,现计划用这两种布料生产![]() 、
、![]() 两种型号的时装共80套.已知做一套
两种型号的时装共80套.已知做一套![]() 型号的时装需用A种布料1.1米,
型号的时装需用A种布料1.1米,![]() 种布料0.4米,可获利50元;做一套
种布料0.4米,可获利50元;做一套![]() 型号的时装需用
型号的时装需用![]() 种布料0.6米,
种布料0.6米,![]() 种布料0.9米,可获利45元.设生产
种布料0.9米,可获利45元.设生产![]() 型号的时装套数为
型号的时装套数为![]() ,用这批布料生产两种型号的时装所获得的总利润为
,用这批布料生产两种型号的时装所获得的总利润为![]() 元.
元.
(1)求![]() (元)与
(元)与![]() (套)的函数关系式.
(套)的函数关系式.
(2)有几种生产方案?
(3)如何生产使该厂所获利润最大?最大利润是多?
【答案】(1)y=5x+3600;(2)共有5种生产方案;(3)当生产![]() 型号的时装44套、生产
型号的时装44套、生产![]() 型号的时装36套时,该厂所获利润最大,最大利润为3820元.
型号的时装36套时,该厂所获利润最大,最大利润为3820元.
【解析】
(1)根据题意,根据总利润=![]() 型号的总利润+
型号的总利润+![]() 型号的总利润,即可求出
型号的总利润,即可求出![]() (元)与
(元)与![]() (套)的函数关系式;
(套)的函数关系式;
(2)根据A、B两种布料的总长列出不等式,即可求出x的取值范围,从而求出各个方案;
(3)一次函数的增减性,求最值即可.
解:(1)由题意可知:y=50x+45(80-x)=5x+3600
即![]() (元)与
(元)与![]() (套)的函数关系式为y=5x+3600;
(套)的函数关系式为y=5x+3600;
(2)由题意可知:
解得:![]()
故可生产![]() 型号的时装40套、生产
型号的时装40套、生产![]() 型号的时装80-40=40套或生产
型号的时装80-40=40套或生产![]() 型号的时装41套、生产
型号的时装41套、生产![]() 型号的时装80-41=39套或生产
型号的时装80-41=39套或生产![]() 型号的时装42套、生产
型号的时装42套、生产![]() 型号的时装80-42=38套或生产
型号的时装80-42=38套或生产![]() 型号的时装43套、生产
型号的时装43套、生产![]() 型号的时装80-43=37套或生产
型号的时装80-43=37套或生产![]() 型号的时装44套、生产
型号的时装44套、生产![]() 型号的时装80-44=36套,共5种生产方案
型号的时装80-44=36套,共5种生产方案
答:共有5种生产方案.
(3)∵一次函数y=5x+3600中,![]() ,5>0
,5>0
∴y随x的增大而增大
∴当x=44时,y取最大值,ymax=44×5+3600=3820
即当生产![]() 型号的时装44套、生产
型号的时装44套、生产![]() 型号的时装36套时,该厂所获利润最大,最大利润为3820元.
型号的时装36套时,该厂所获利润最大,最大利润为3820元.
答: 当生产![]() 型号的时装44套、生产
型号的时装44套、生产![]() 型号的时装36套时,该厂所获利润最大,最大利润为3820元.
型号的时装36套时,该厂所获利润最大,最大利润为3820元.

【题目】为了传承中华优秀传统文化,市教育局决定开展“经典诵读进校园”活动,某校团委组织八年级100名学生进行“经典诵读”选拔赛,赛后对全体参赛学生的成绩进行整理,得到下列不完整的统计图表。
组别 | 分数段 | 频次 | 频率 |
A | 60x<70 | 17 | 0.17 |
B | 70x<80 | 30 | a |
C | 80x<90 | b | 0.45 |
D | 90x<100 | 8 | 0.08 |
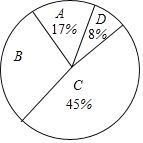
请根据所给信息,解答以下问题:
(1)表中a=___,b=___;
(2)请计算扇形统计图中B组对应扇形的圆心角的度数;
(3)已知有四名同学均取得98分的最好成绩,其中包括来自同一班级的甲、乙两名同学,学校将从这四名同学中随机选出两名参加市级比赛,请用列表法或画树状图法求甲、乙两名同学都被选中的概率。