题目内容
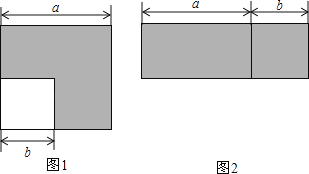
【题目】已知梯形ABCD中,AD∥BC,AB=AD(如图所示).
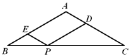
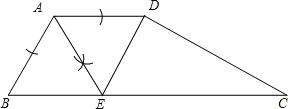
(1)在下图中,用尺规作∠BAD的平分线AE交BC于点E,连接DE(保留作图痕迹,不写作法),并证明四边形ABED是菱形;
(2)若∠ABC=60°,EC=2BE.求证:ED⊥DC.

【答案】(1)作图见解析;证明见解析;(2)证明见解析.
【解析】
(1)、根据尺规作图:角的平分线的基本作法,可得到∠BAD的平分线AE;利用菱形的判定定理,即可证得;(2)、根据直角三角形的性质定理,可得△EDC是直角三角形,即可得ED⊥DC.
(1)解:作图如图所示.在△ABE与△ADE中,∵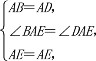
∴△ABE≌△ADE,∴∠AEB=∠AED.∵AD∥BE,∴∠AEB=∠DAE,∴∠BAE=∠AED,
∴AB∥DE,∴四边形ABED是平行四边形.∵AB=AD,∴四边形ABED为菱形;
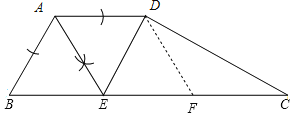
(2)证明:取EC的中点F,连接DF.
∵四边形ABED是菱形,∴EC=2BE=2DE=2EF=2CF,∠CED=∠ABC=60°,
∴△DEF是等边三角形,∴DF=EF=CF,∠DFE=60°,
∴∠CDF+∠C=∠DFE=60°=2∠C.即∠C=30°,
∴∠EDC=180°-∠CED-∠C=90°,即ED⊥DC.

 名校课堂系列答案
名校课堂系列答案【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6 | a | b | x | -2 | 1 | … |
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.