题目内容
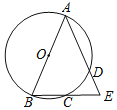
【题目】如图,点A,B,C,D在⊙O上,弦AD的延长线与弦BC的延长线相交于点E.用①AB是⊙O的直径,②CB=CE,③AB=AE中的两个作为题设,余下的一个作为结论组成一个命题,则组成真命题的个数为( )
A.0B.1C.2D.3
【答案】D
【解析】
根据题意和图形,可以写出其中的两个为题设,一个为结论时的命题是否为真命题,然后写出理由即可.
解:当①②为题设时,③为结论,这个命题是真命题,
理由:
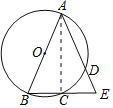
连接AC
∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠ACE=90°,
在△ACB和△ACE中,
 ,
,
∴△ACB≌△ACE(SAS),
∴AB=AE;
当①③为题设,②为结论时,这个命题是真命题,
理由:∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠ACB=∠ACE=90°,
在Rt△ACB和Rt△ACE中,
![]() ,
,
∴Rt△ACB≌Rt△ACE(HL),
∴CB=CE;
当②③为题设,①为结论时,这个命题是真命题,
理由:在△ACB和△ACE中,
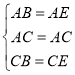 ,
,
∴△ACB≌△ACE(SSS),
∴∠ACB=∠ACE,
又∵∠ACB+∠ACE=180°,
∴∠ACB=∠ACE=90°,
∴AB是⊙O的直径;
故选:D.

练习册系列答案
相关题目