题目内容
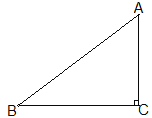
【题目】如图,△ABC中,∠ACB=90°,AB=5cm,BC=4cm,若点P从点A出发,以每秒2cm的速度沿折线A﹣B﹣C﹣A运动,设运动时间为t秒(t>0).
(1)若点P在BC上,且满足PA=PB,求此时t的值;
(2)若点P恰好在∠ABC的角平分线上,求此时t的值;
【答案】(1)![]() s;(2)
s;(2)![]() s.
s.
【解析】
(1)点P在BC上,故设点P在BC上运动的长度为2t1,即BP=2t1,此时的t=![]() +2t1,∵PA=PB,从而根据勾股定理列出关于t1的方程;(2)由题意可知:点P在AC上,设点P在AC上运动的长度为2t2,此时的t=
+2t1,∵PA=PB,从而根据勾股定理列出关于t1的方程;(2)由题意可知:点P在AC上,设点P在AC上运动的长度为2t2,此时的t=![]() +2t2,过P作PD⊥AB,根据角平分线的性质可得:PC=PD,∴易证明△CPB≌△DPB,从而根据勾股定理列出关于t2的方程.
+2t2,过P作PD⊥AB,根据角平分线的性质可得:PC=PD,∴易证明△CPB≌△DPB,从而根据勾股定理列出关于t2的方程.
(1)如图,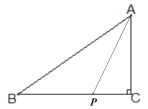 ,在Rt△ABC中,可得:AC=
,在Rt△ABC中,可得:AC=![]() =3,∵PB=PA=2t1,∴在Rt△APC中,(2t1)2=32+(4-2t1)2,解得:t1=
=3,∵PB=PA=2t1,∴在Rt△APC中,(2t1)2=32+(4-2t1)2,解得:t1=![]() ,故t=
,故t=![]() +
+![]() =
=![]() s;
s;
(2)如图,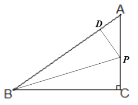 ,∵角平分线性质可得:PC=PD=2t2,而∵PD⊥AB,∴∠PDB=∠PCB=90°,∵PB平分∠ABC,∴∠DBP=∠CBP,∴∠BPC=∠BPD,在△PBC和△PBD中,
,∵角平分线性质可得:PC=PD=2t2,而∵PD⊥AB,∴∠PDB=∠PCB=90°,∵PB平分∠ABC,∴∠DBP=∠CBP,∴∠BPC=∠BPD,在△PBC和△PBD中, ,∴△PBC≌△PBD,∴BC=BD,在Rt△ADP中,AD=5-4=1,∴(3-2t2)2=12+(2t2)2,解得:t2=
,∴△PBC≌△PBD,∴BC=BD,在Rt△ADP中,AD=5-4=1,∴(3-2t2)2=12+(2t2)2,解得:t2=![]() ,故t=
,故t=![]() +
+![]() =
=![]() s.
s.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目