题目内容
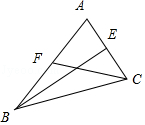
【题目】在△ABC中,若3sinC=2sinB,点E,F分别是AC,AB的中点,则 ![]() 的取值范围为 .
的取值范围为 .
【答案】![]()
【解析】解:∵3sinC=2sinB,可得:3AB=2AC,即:AC= ![]() AB, 又∵点E,F分别是AC,AB的中点,
AB, 又∵点E,F分别是AC,AB的中点,
∴AE= ![]() AC,AF=
AC,AF= ![]() ,
,
∴在△ABE中,由余弦定理可得:BE2=AB2+AE2﹣2ABAEcosA
=AB2+( ![]() AB)2﹣2AB
AB)2﹣2AB ![]() ABcosA
ABcosA
= ![]() AB2﹣
AB2﹣ ![]() AB2cosA,
AB2cosA,
在△ACF中,由余弦定理可得:CF2=AF2+AC2﹣2AFACcosA
=( ![]() AB)2+(
AB)2+( ![]() AB)2﹣2
AB)2﹣2 ![]() AB
AB ![]() ABcosA
ABcosA
= ![]() AB2﹣
AB2﹣ ![]() AB2cosA,
AB2cosA,
∴ ![]() =
= 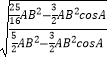 =
= ![]() ,
,
∵A∈(0,π),
∴cosA∈(﹣1,1),可得: ![]() ∈(
∈( ![]() ,
, ![]() ),
),
∴可得: ![]() =
= ![]() ∈
∈ ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解正弦定理的定义的相关知识,掌握正弦定理:![]() .
.

练习册系列答案
相关题目



