题目内容
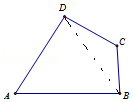
【题目】如图，A，B，C，D为平面四边形ABCD的四个内角，若A+C=180°，AB=6，BC=4，CD=5，AD=5，则四边形ABCD面积是 ． 
【答案】10 
【解析】解：连结BD， 在△ABD中，BD2=AB2+AD2﹣2ABADcosA=61﹣60cosA，
在△BCD中，BD2=BC2+CD2﹣2BCCDcosC=41﹣40cosC．
∴61﹣60cosA=41﹣40cosC，
∵A+C=180°，
∴cosA=﹣cosC．
∴cosA= 
．
∴sinA=sinC= 
．
∴四边形ABCD的面积S=S△ABD+S△BCD= 
AB×AD×sinA+ BC×CD×sinC
= 
6×5× + ×4×5× =10
所以答案是：10 
练习册系列答案
能考试期末冲刺卷系列答案
相关题目
