Question

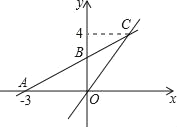
【题目】如图，在平面直角坐标系xOy中，O是坐标原点，一次函数y＝kx+b的图象与x轴交于点A（﹣3，0），与y轴交于点B，且与正比例函数y＝x的图象的交点为C（m，4）．

（1）求一次函数y＝kx+b的解析式；

（2）D是平面内一点，以O、C、D、B四点为顶点的四边形是平行四边形，直接写出点D的坐标．（不必写出推理过程）．

Answer 1

【答案】(1) y＝x+2;(2)（﹣3，﹣2）、（3，2）、（3，6）

【解析】

（1）先把点C的坐标代入正比例函数关系式，可求出m的值，再把点A，C的坐标代入一次函数的解析式求出k，b即可．

（2）利用CD平行且等于OD，或BODC进而求解．

解：（1）把点C（m，4），代入正比例函数y＝x得，

4＝m，解得m＝3，

∴点C的坐标为（3，4），

∵A的坐标为（﹣3，0）

∴

解得

∴一次函数的解析式为：y＝x+2．

（2）∵O、C、D、B四点为顶点的四边形是平行四边形，

∴只要CO平行且等于BD，即BD＝5，

①当点D在点O的左边时，点D的坐标为（﹣3，﹣2），

②当点D在点O的右边时，点D的坐标为（3，2），

③当BO∥DC时，D（3，6）

∴点D的坐标为（﹣3，﹣2）、（3，2）、（3，6）．