Question

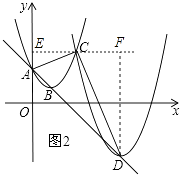
【题目】如图1，已知直线l：y=﹣x+2与y轴交于点A，抛物线y=（x﹣1）2+k经过点A，其顶点为B，另一抛物线y=（x﹣h）2+2﹣h（h＞1）的顶点为D，两抛物线相交于点C．

（1）求点B的坐标，并说明点D在直线l上的理由；
（2）设交点C的横坐标为m．
交点C的纵坐标可以表示为：或；
（3）如图2，若∠ACD=90°，求m的值．

Answer 1

【答案】
（1）

解：当x=0时候，y=﹣x+2=2，

∴A（0，2），

把A（0，2）代入y=（x﹣1）2+k，得1+k=2

∴k=1，

∴y=（x﹣1）2+1，

∴B（1，1）

∵D（h，2﹣h）

∴当x=h时，y=﹣x+2=﹣h+2=2﹣h

∴点D在直线l上

（2）（m﹣1）2+1；（m﹣h）2﹣h+2
（3）解：过点C作y轴的垂线，垂足为E，过点D作DF⊥CE于点F

∵∠ACD=90°，

∴∠ACE=∠CDF

又∵∠AEC=∠DFC

∴△ACE∽△CDF

∴

又∵C（m，m2﹣2m+2），D（2m，2﹣2m），

∴AE=m2﹣2m，DF=m2，CE=CF=m

∴ =

∴m2﹣2m=1

解得：m=± +1

∵h＞1

∴m= ＞

∴m= +1

【解析】解： （2）（m﹣1）2+1或（m﹣h）2﹣h+2
由题意得（m﹣1）2+1=（m﹣h）2﹣h+2，
整理得2mh﹣2m=h2﹣h
∵h＞1
∴m= = ．