题目内容
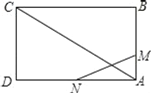
【题目】如图，矩形ABCD的边长AB＝3cm，AC＝3
cm，动点M从点A出发，沿AB以1cm/s的速度向点B匀速运动，同时动点N从点D出发，沿DA以2cm/s的速度向点A匀速运动．若△AMN与△ACD相似，则运动的时间t为_____s．
【答案】1.5或2.4
【解析】
先假设相似，利用相似中的比例线段列出方程，有解的且符合题意的t值即可说明存在，反之则不存在．
因为四边形ABCD是矩形，得△ADC是直角三角形，CD=AB，
所以，
,
由题意得DN＝2t，AN＝6﹣2t，AM＝t，
若△NMA∽△ACD，
则有
＝
，即
＝
，
解得t＝1.5秒，
若△MNA∽△ACD
则有
＝
，即
＝
，
解得t＝2.4秒，
答：当t＝1.5秒或2.4秒时，△AMN与△ACD相似．
故答案为：1.5或2.4．
练习册系列答案
相关题目
【题目】茶叶是安徽省主要经济作物之一，2020年新茶上市期间，某茶厂为获得最大利益，根据市场行情，把新茶价格定为400元/kg，并根据历年的相关数据整理出第x天（1≤x≤15，且x为整数）制茶成本（含采摘和加工）和制茶量的相关信息如下表．假定该茶厂每天制作和销售的新茶没有损失，且能在当天全部售出（当天收入=日销售额-日制茶成本）
制茶成本（元/kg） | 150+10x |
制茶量（kg） | 40+4x |
（1）求出该茶厂第10天的收入；
（2）设该茶厂第x天的收入为y（元）．试求出y与x之间的函数关系式，并求出y的最大值及此时x的值．
