题目内容
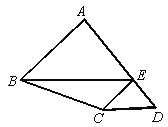
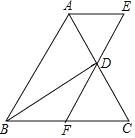
【题目】如图,△ABC 是等边三角形,D 为 AC 上一点连接 BD,旋转△BCD,使点 B 落在 BC上方的点 E 处,点 C 落在 BC 上的点 F 处,点 D 落在点 C 处,连接 AE.
求证:四边形 ABFE 是平行四边形.
【答案】详见解析.
【解析】
由题意△ABC、△AED、△DCF是等边三角形,可以推知同位角∠CFD=∠ABC,内错角∠CFD=∠AED.所以利用平行的线的判定定理可以证得四边形ABFE的对边相互平行.
证明:∵△ABC 是等边三角形,
∴AC=BC=AB,∠ACB=60°
∵将 AC 绕点 E 旋转
∴DF=DC,DE=DA
∴△DFC 是等边三角形,
∴DF=CD=CF,∠DCF=∠EFC=60°,
∴EF=AC=BC,
∴△ABC、△AED、△DCF 均为等边三角形,
∴∠CFD=∠ABC=∠DEA=60°,
∴AB∥EF,BF∥AE,
∴四边形 ABFE 是平行四边形.

练习册系列答案
相关题目