题目内容
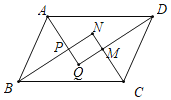
【题目】如图,正方形![]() 的边长为6个单位长度,点
的边长为6个单位长度,点![]() 是
是![]() 边的中点,点
边的中点,点![]() 从点
从点![]() 出发,以1个单位/秒的速度按
出发,以1个单位/秒的速度按![]() 的方向运动,再次回到
的方向运动,再次回到![]() 点结束运动,设
点结束运动,设![]() 点运动的时间为
点运动的时间为![]() 秒.
秒.


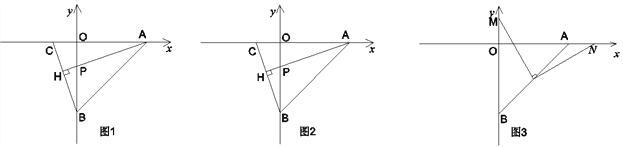
(1)如图1,若![]() 为直角三角形,求
为直角三角形,求![]() 的值;
的值;
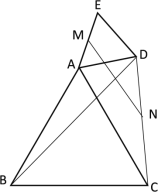
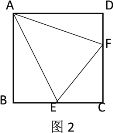
(2)如图2,若点![]() 在
在![]() 上,且
上,且![]() ,求
,求![]() 的度数;
的度数;
(3)如图3,点![]() 是对角线
是对角线![]() 的三等分点,且
的三等分点,且![]() ,若
,若![]() ,直接写出满足条件的
,直接写出满足条件的![]() 点的个数,并注明这些
点的个数,并注明这些![]() 点分别在正方形的哪条边上.
点分别在正方形的哪条边上.
【答案】(1)4.5或12或21;(2)135°;(3)有两个,分别在![]() 和
和![]() 上
上
【解析】
(1)分当点F在CD上、AD上以及和点B重合时三种情况分别求出相应的t值;
(2)根据题意求出DF和CF,EF,延长![]() 至点
至点![]() ,证明
,证明![]() ,得到
,得到![]() ,
,![]() ,再证明
,再证明![]() ,得到对应角相等,最后根据
,得到对应角相等,最后根据![]() 可得结果;
可得结果;
(3)分点F在正方形各边上的情况,分别求出![]() 的最值,即可得出结果.
的最值,即可得出结果.
解:(1)①当点![]() 在
在![]() 上,
上,![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]() ,
,
解之:![]() ,
,
②当点![]() 在
在![]() 上,
上,![]() ,
,![]() ,
,
③当点![]() 与
与![]() 点重合,
点重合,![]() ,
,![]() ,
,
(2)解:∵![]() ,
,
∴![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
延长![]() 至点
至点![]() ,使
,使![]() ,
,
则![]() ,
,
在![]() 与
与![]() 中,
中,
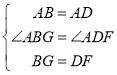 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 与
与![]() 中,
中,
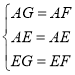 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
又∵在![]() 中,
中,![]() ,
,
∴![]() ;
;
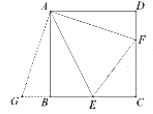
(3)满足条件的![]() 点有两个,分别在
点有两个,分别在![]() 边和
边和![]() 上.
上.
理由是:当点F在AB上时,如图,
E′为点E关于AB的对称点,GH⊥BC于H,
∵GH∥CD,
∴![]() ,
,
可得GH=BH=4,
∴![]() 的最小值为E′G=
的最小值为E′G=![]() >8,
>8,
即AB上没有符合要求的F;
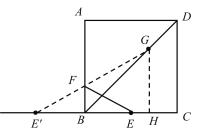
当点F在AD上时,如图,
E′为点E关于AD的对称点,
同理可得:KG=![]() AB=2,HG=6+2=8<E′G,
AB=2,HG=6+2=8<E′G,
∴此时![]() 的最小值为E′G的长,大于8,
的最小值为E′G的长,大于8,
∴AD上不存在符合要求的F;

当点F在CD上时,如图,
E′为点E关于CD的对称点,GH⊥BC于H,
同理可得:GH=BH=4,HC=2,
∴HE′=5,
此时![]() 的最小值为E′G=
的最小值为E′G=![]() <8,
<8,
当点F在点D处时,![]() =ED+GD=
=ED+GD=![]() =
=![]() ,
,
∴CD上存在符合要求的点F;
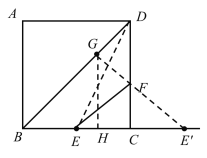
当点F在BC上时,GH⊥BC于H,
若点F与点E重合,
同理可知GH=4=BH,EH=BH-BE=1,
则![]() =GE=
=GE=![]() <8,
<8,
若点F与点B重合,
同理可知BG=![]() ,BE=3,
,BE=3,
则![]() =BE+BG=
=BE+BG=![]() =8,
=8,
故BC上存在符合要求的点F;
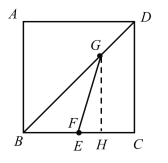
综上:满足条件的![]() 点有两个,分别在
点有两个,分别在![]() 和
和![]() 上.
上.