Question

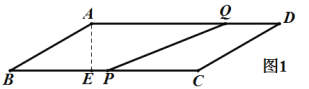
【题目】如图，在平行四边形 ABCD中，AB 6cm ，BC 12cm ，B 30，点P 在 BC 上由点B向点C 出发，速度为每秒2cm；点Q 在边AD上，同时由点 D 向点 A 运动，速度为每秒1cm ，当点 P 运动到点C时，P 、Q 同时停止运动，连接 PQ，设运动时间为t秒．

（1）当t为何值时四边形 ABPQ 为平行四边形？

（2）当t为何值时，四边形 ABPQ 的面积是四边形 ABCD 的面积的四分之三？

（3）连接 AP ，是否存在某一时刻t，使ABP 为等腰三角形？并求出此刻t的值．

Answer 1

【答案】（1）当时，四边形是平行四边形；（2）当时，四边形的面积是四边形的面积的四分之三；（3）存在，当或或时，为等腰三角形

【解析】

（1）利用平行四边形的对边相等得，建立方程求解即可；

（2）分别表示出四边形ABPQ和四边形ABCD的面积，利用面积关系即可求出；

（3）分三种情况，利用等腰三角形的性质，两腰相等建立方程求解即可得出结论．

解：（1）由P、Q的运动方式得：cm，cm，

∵当点P运动到点C时，P、Q同时停止运动，

∴，

在平行四边形 ABCD中，BC 12cm，

∴cm，则cm，

若四边形 ABPQ 为平行四边形，

则，

即，解得：，

∴当时，四边形是平行四边形；

（2）如图 1，过点作于，

在中，，cm，

cm，

四边形是平行四边形，BC 12cm，

∴cm2，

由（1）得：cm，cm，

∴S四边形ABPQ=cm2，

若四边形的面积是四边形的面积的四分之三，

即，解得：，

∴当时，四边形的面积是四边形的面积的四分之三；

（3）存在某一时刻t，使为等腰三角形,

若为等腰三角形，则或或，

①当时，则cm，

即，解得：；

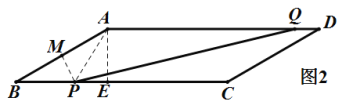
②当时， 如图 2 ，过作垂直于，垂足为点，

∵，⊥，

∴cm，

，

∴cm，

则，解得：，

③当时，如图3，

∵，，

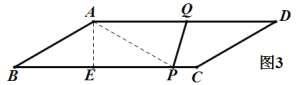
∴E为BP中点，则BP=2BE，

在中，，cm，AE=3cm，

∴cm，cm，

则，解得：，

所以，当或或时，为等腰三角形．