Question

【题目】如图，四边形ABCD是正方形，点E在直线BC上，连接AE．将△ABE沿AE所在直线折叠，点B的对应点是点B′，连接AB′并延长交直线DC于点F．

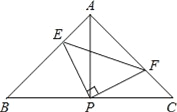
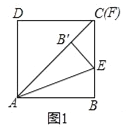
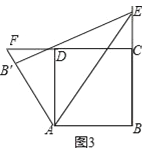
（1）当点F与点C重合时如图1，证明：DF+BE=AF；

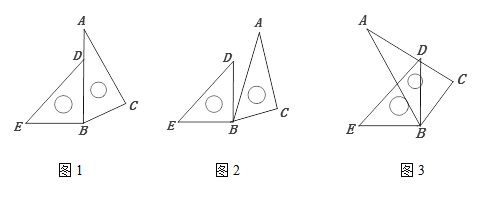
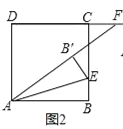
（2）当点F在DC的延长线上时如图2，当点F在CD的延长线上时如图3，线段DF、BE、AF有怎样的数量关系？请直接写出你的猜想，并选择一种情况给予证明．

Answer 1

【答案】（1）证明见解析（2）证明见解析

【解析】试题分析：（1）由折叠可得AB＝AB′，BE＝B′E，再根据四边形ABCD是正方形，易证B′E＝B′F，即可证明DF＋BE＝AF；

（2）图（2）的结论：DF＋BE＝AF；图（3）的结论：BE－DF＝AF；证明图（2）：延长CD到点G，使DG＝BE，连接AG，需证△ABE≌△ADG，根据CB∥AD，得∠AEB＝∠EAD，即可得出∠B′AE＝∠DAG，则∠GAF＝∠DAE，则∠AGD＝∠GAF，即可得出答案BE＋DF＝AF．

试题解析：

解：（1）由折叠可得AB＝AB′，BE＝B′E，

∵四边形ABCD是正方形，

∴AB＝DC＝DF，∠B′CE＝45°，

∴B′E＝B′F，

∴AF＝AB′＋B′F，

即DF＋BE＝AF；

（2）图（2）的结论：DF＋BE＝AF；

图（3）的结论：BE﹣DF＝AF；

图（2）的证明：延长CD到点G，使DG＝BE，连接AG，

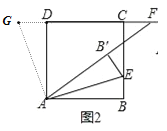
易证△ABE≌△ADG，

∴∠BAE＝∠DAG，∠AEB＝∠AGD，

∵∠BAE＝∠B′AE，

∴∠B′AE＝∠DAG，

∴∠GAF＝∠DAE，

∵CB∥AD，

∴∠AEB＝∠EAD，

∴∠AGD＝∠GAF，

∴GF＝AF，

∴BE＋DF＝AF；

图（3）的证明：在BC上取点M，使BM＝DF，连接AM，

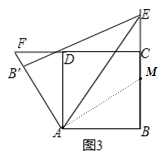
易证△ABM≌△ADF，

∴∠BAM＝∠FAD，AF＝AM，

∵△ABE≌AB′E，

∴∠BAE＝∠EAB′，

∴∠MAE＝∠DAE，

∵AD∥BE，

∴∠AEM＝∠DAB，

∴∠MAE＝∠AEM，

∴ME＝MA＝AF，

∴BE﹣DF＝AF．