题目内容
【题目】阅读材料并回答下列问题：
在平面直角坐标系 xOy 中， 点 P x, y 经过 f 变换得到点 P x, y ， 变换记作f x, y x, y， 其中
，例如，当a=1，b=1时，则点（-1，2）经过f变换，
，即
.
（1）当 a 1， b 1时，则 f 0, 1 .
（2）若 f 2,3 4, 2 ，求 a 和b 的值.
（3）若象限内点 P x, y 的横纵坐标满足 y 3x ，点 P 经过 f 变换得到点 P x, y，若点 P 与点 P重合，求 a 和b 的值.
【答案】（1）（1，1）；（2）
；（3）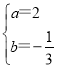
.
【解析】
（1）将a＝1，b＝1，f（0，1）代入
，可求x′，y′的值，从而求解；
（2）将f（2，3）＝（4，2）代入，可得关于a，b的二元一次方程组，解方程组即可求解；
（3）由点P（x，y）经过变换f得到的对应点P'（x'，y'）与点P重合，点P（x，y）在直线y＝3x上，可得f（x，y）＝（x，y），f（x，3x）＝（x，3x），得到关于a，b的二元一次方程组，解方程组即可求解．
解：（1）当a＝1，b＝1时，
x′＝1×0＋（1）×（1）＝1，y′＝1×0（1）×（1）＝1，
则f（0，1）＝（1，1）；
故答案为：（1，1）；
（2）∵f（2，3）＝（4，2），
∴
，
解得；
（3）∵点P（x，y）经过变换f得到的对应点P'（x'，y'）与点P重合，
∴f（x，y）＝（x，y）．
∵点P（x，y）在直线y＝3x上，
∴f（x，3x）＝（x，3x）．
∴
，
即
，
∵x为任意的实数，
∴
，
解得．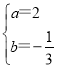
练习册系列答案
相关题目
