题目内容
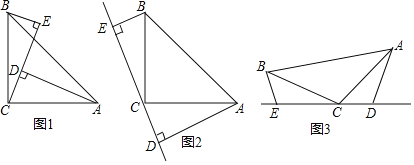
【题目】如图,在正方形![]() 中,点
中,点![]() 是对角线
是对角线![]() 上一点,且
上一点,且![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)求证:![]() ;
;
(2)当![]() 时,求
时,求![]() 的值.
的值.
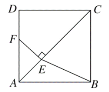
【答案】(1)详见解析;(2)4+4![]()
【解析】
(1)连接CF,利用HL证明Rt△CDF≌Rt△CEF,可得DF=EF,再根据等腰直角三角形可得EF=AF,所以得出DF=AE.
(2) 过点E作EH⊥AB于H,利用勾股定理求出AC,再求出AE,根据特殊直角三角形的边长比求出EH和AH,可得BH,再利用勾股定理求出BE2即可.
(1)连接CF,
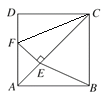
∵∠D=∠CEF=90°,CD=CE,CF=CF,
∴Rt△CDF≌Rt△CEF(HL),
∴DF=EF,
∵AC为正方形ABCD的对角线,
∴∠CAD=45°,
∴△AEF为等腰直角三角形,
∴EF=AF,
∴DF=AE.
(2) ∵AB=2+![]() ,
,
∴由勾股定理得AC=2![]() +2,
+2,
∵CE=CD,
∴AE=![]() .
.
过点E作EH⊥AB于H,则△AEH是等腰直角三角形.
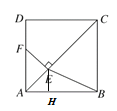
∴EH=AH=![]() AE=
AE=![]() ×
×![]() =1.
=1.
∴BH=2+![]() -1=1+
-1=1+![]() .
.
在Rt△BEH中,BE2=BH2+EH2=(1+![]() )2+12=4+4
)2+12=4+4![]() .
.

练习册系列答案
相关题目