Question

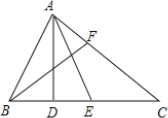
【题目】如图，在△ABC中，∠B=90°，AB=6厘米，BC=8厘米．点P从A点开始沿AB边向点B以1厘米/秒的速度移动（到达点B即停止运动），点Q从B点开始沿BC边向点C以2厘米/秒的速度移动（到达点C即停止运动）．

(1)如果P，Q分别从A，B两点同时出发，经过几秒钟，△PBQ的面积等于△ABC面积的三分之一?

(2)如果P，Q两点分别从A，B两点同时出发，几秒钟后，P，Q相距6厘米?

Answer 1

【答案】(1) 2 秒或4秒；(2) 0秒或2.4秒．

【解析】

（1）设经过x秒钟，△PBQ的面积等于是△ABC的三分之一，分别表示出线段PB和线段BQ的长，然后根据面积之间的关系列出方程求得时间即可；

（2）根据勾股定理列出方程求解即可；

（1）设t秒后，△PBQ的面积等于是△ABC的三分之一，根据题意得：

×2t（6-t）=××6×8，

解得：t=2或4．

答：2秒或4秒后，△PBQ的面积等于是△ABC的三分之一．

（2）设x秒时，P、Q相距6厘米，根据题意得：

（6-x）2+（2x）2=36，

解得：x=0或x=．

答：0秒或秒时，P、Q相距6厘米．