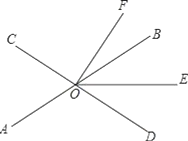
��Ŀ����
����Ŀ����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC=65������һֱ�������ε�ֱ�����ǰ��ֱ�Ƕ�����ڵ�O��.
��1����ͼ1�������ǰ�MON��һ��ON������OB�غϣ����MOC=___________��
��2����ͼ2�������ǰ�MON�Ƶ�O��ʱ����תһ���Ƕȣ���ʱOC�ǡ�MOB�Ľ�ƽ���ߣ�����ת�ǡ�BON�͡�CON�Ķ�����

��3�������ǰ�MON�Ƶ�O��ʱ����ת��ͼ3ʱ����NOC=![]() ��AOM�����NOB�Ķ���.
��AOM�����NOB�Ķ���.
���𰸡���1��25����2��25����3��70��
�������������������1�����ݡ�MON�͡�BOC�Ķ������Եõ���MON�Ķ�����
��2�����ݽ�ƽ���ߵ����ʣ��ɡ�BOC=65�㣬������á�BOM�Ķ�����Ȼ���ɡ�NOM-90�㣬�ɵá�BON�Ķ������Ӷ��ý⣻
��3���ɡ�BOC=65������NOM=90������NOC=![]() ��AOM���Ӷ�����á�NOC�Ķ�����Ȼ���ɡ�BOC=65�㣬�Ӷ��ý�.
��AOM���Ӷ�����á�NOC�Ķ�����Ȼ���ɡ�BOC=65�㣬�Ӷ��ý�.
�����������1��![]() ��MON=90����BOC=65��
��MON=90����BOC=65��
![]() ��MOC=��MON-��BOC=90��-65��=25��
��MOC=��MON-��BOC=90��-65��=25��
��2��![]() ��BOC=65�㣬OCƽ�֡�MOB
��BOC=65�㣬OCƽ�֡�MOB
![]() ��MOB=2��BOC=130��
��MOB=2��BOC=130��
![]() ��BON=��MOB-��MON=130��-90��=40��
��BON=��MOB-��MON=130��-90��=40��
![]() ��CON=��COB-��BON=65��-40��=25��
��CON=��COB-��BON=65��-40��=25��
��3��![]() ��NOC=
��NOC=![]() ��AOM
��AOM ![]() ��AOM=4��NOC
��AOM=4��NOC ![]() ��BOC=65��
��BOC=65��
![]() ��AOC=��AOB-��BOC=180��-65��=115��
��AOC=��AOB-��BOC=180��-65��=115��
![]() ��MON=90��
��MON=90��
![]() ��AOM+��NOC=��AOC-��MON=115��-90��=25��
��AOM+��NOC=��AOC-��MON=115��-90��=25��
![]() 4��NOC+��NOC=25��
4��NOC+��NOC=25��
![]() ��NOC=5��
��NOC=5��
![]() ��NOB=��NOC+��BOC=70��
��NOB=��NOC+��BOC=70��

 ��ѧ��ʦ����ϵ�д�
��ѧ��ʦ����ϵ�д�����Ŀ��ij��˾��ÿ��![]() Ԫ�ļ۸��չ���
Ԫ�ļ۸��չ���![]() ��ij��ҩ�ģ���ֱ�����г������ۣ�ÿ�ֵ��ۼ���
��ij��ҩ�ģ���ֱ�����г������ۣ�ÿ�ֵ��ۼ���![]() Ԫ���ù�˾�����ӹ����ٳ��ۣ������Ϣ���±���ʾ��
Ԫ���ù�˾�����ӹ����ٳ��ۣ������Ϣ���±���ʾ��
���� | ÿ��ɼӹ�ҩ�ĵĶ��� | ��Ʒ�� | ��Ʒ�ۼ� ��Ԫ/���� |
�ּӹ� | 14 | 80% | 6000 |
���ӹ� | 6 | 60% | 11000 |
(ע:����Ʒ��80%ָ�ӹ�100��ԭ���ܵõ�80�ֿ�����ҩ�ģ��ڼӹ���ķ�Ʒ������Ч��.)
���г�Ӱ�죬�ù�˾������![]() ���ڽ�����ҩ�ļӹ���ϣ�
���ڽ�����ҩ�ļӹ���ϣ�
��1����ȫ���ּӹ����ɻ���_______________________Ԫ��
��2���������ܶ�ľ��ӹ���ʣ���ֱ�����г������ۣ��ɻ���_____________Ԫ��
��3�������ִּӹ������־��ӹ���ǡ��![]() ����ɣ���ɻ�������Ԫ?
����ɣ���ɻ�������Ԫ?