题目内容
【题目】在平面直角坐标系xOy中,抛物线y=x2+bx+c与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,点B的坐标为(3,0),将直线y=kx沿y轴向上平移3个单位长度后恰好经过B,C两点.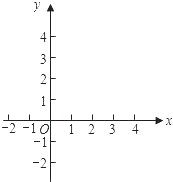
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;
(3)连接CD,求∠OCA与∠OCD两角和的度数.
【答案】
(1)解:∵y=kx沿y轴向上平移3个单位长度后经过y轴上的点C, 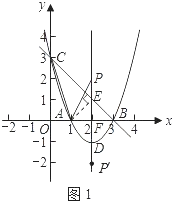
∴C(0,3).
设直线BC的解析式为y=kx+3.
∵B(3,0)在直线BC上,
∴3k+3=0.
解得k=﹣1.
∴直线BC的解析式为y=﹣x+3.
∵抛物线y=x2+bx+c过点B,C,
∴ ![]()
解得 ![]() ,
,
∴抛物线的解析式为y=x2﹣4x+3.
(2)解:由y=x2﹣4x+3.
可得D(2,﹣1),A(1,0).
∴OB=3,OC=3,OA=1,AB=2.
可得△OBC是等腰直角三角形,
∴∠OBC=45°,CB=3 ![]() .
.
如图1,设抛物线对称轴与x轴交于点F,
∴AF= ![]() AB=1.
AB=1.
过点A作AE⊥BC于点E.
∴∠AEB=90度.
可得BE=AE= ![]() ,CE=2
,CE=2 ![]() .
.
在△AEC与△AFP中,∠AEC=∠AFP=90°,∠ACE=∠APF,
∴△AEC∽△AFP.
∴ ![]() ,
, ![]() .
.
解得PF=2.∵点P在抛物线的对称轴上,
∴点P的坐标为(2,2)或(2,﹣2).
(3)解:解法一:
如图2, 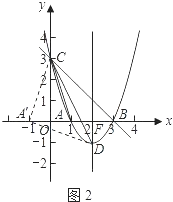
作点A(1,0)关于y轴的对称点A',则A'(﹣1,0).
连接A'C,A'D,
可得A'C=AC= ![]() ,∠OCA'=∠OCA.
,∠OCA'=∠OCA.
由勾股定理可得CD2=20,A'D2=10.
又∵A'C2=10,
∴A'D2+A'C2=CD2.
∴△A'DC是等腰直角三角形,∠CA'D=90°,
∴∠DCA'=45度.
∴∠OCA'+∠OCD=45度.
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.
解法二:
如图3,连接BD. 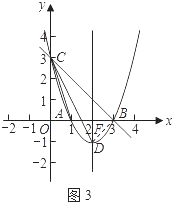
同解法一可得CD= ![]() ,AC=
,AC= ![]() .
.
在Rt△DBF中,∠DFB=90°,BF=DF=1,
∴DB= ![]() .
.
在△CBD和△COA中, ![]() ,
, ![]() ,
, ![]() .
.
∴ ![]() .
.
∴△CBD∽△COA.
∴∠BCD=∠OCA.
∵∠OCB=45°,
∴∠OCA+∠OCD=45度.
即∠OCA与∠OCD两角和的度数为45度.
【解析】直线y=kx向上平移3个单位与y轴交于C,可知C(0,3)代入抛物线解析式即可求出b、c;(2)由∠APD=∠ACB可构造△AEC∽△AFP,由对应边成比例可求出PF,进而求出P坐标;(3)求两角和可转化某一个角然后这两者再相加组成一个角,可由△CBD∽△COA可得出 ∠BCD=∠OCA,∠OCA+∠OCD=∠BCD=45度.
【考点精析】解答此题的关键在于理解相似三角形的判定与性质的相关知识,掌握相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

【题目】某水果商店经销一种苹果,共有20筐,以每筐25千克为标准,超过或不足的千克数分别用正、负数来表示,记录如表:
与标准质量的差值(单位;千克) | -3 | -2 | -1.5 | 0 | 1 | 2.5 |
筐数 | 1 | 4 | 2 | 3 | 2 | 8 |
(1)这20筐苹果中,最重的一筐比最轻的一筐多重多少千克?
(2)与标准重量比较,这20筐苹果总计超过或不足多少千克?
(3)若苹果每千克售价![]() 元,则出售这20筐苹果可卖多少元?
元,则出售这20筐苹果可卖多少元?
【题目】曲靖市某商场投入19200元资金购进甲、乙两种饮料共600箱,饮料的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 36 | 52 |
(1)该商场购进甲、乙两种饮料各多少箱?
(2)全部售完600箱饮料,该商场共获得利润多少元?