题目内容
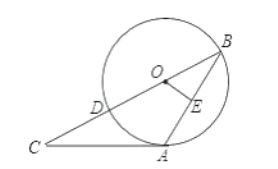
【题目】如果,⊙O是△ABC的外接圆,∠A=45°,BD∥OC交AC的延长线于点D.
(1)求证:BD是⊙O的切线;
(2)若∠D=30°,OC=2.
①求∠ABC的度数;
②求AB的长.
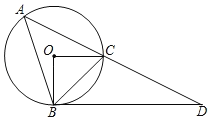
【答案】(1)证明见解析;(2)①60°;②![]() .
.
【解析】
(1)先利用同弧所对的圆周角和圆心角的关系证明∠BOC=90°,再由平行线的性质得出OBD=90°,按照切线的判定定理可得答案;
(2)延长CO交⊙O于点E,连接AE,过C作CH⊥AB于H.①平行线的性质可得∠ACE=∠D=30°,由直径所对的圆周角为直角可得∠EAC=90°,从而可得∠E=60°,再利用同弧所对的圆周角相等可得答案;②由半径的长求得直径的长,利用30°角所对直角边等于斜边的一半,可得AE的长,由勾股定理求得AC的长,利用含45°角的直角三角形和含60°角的直角三角形,可分别求得AH和BH的长,两者相加即可得出AB的长.
(1)证明:∵∠BAC=45°,
∴∠BOC=2∠BAC=90°,
∵BD∥OC,
∴∠BOC+∠OBD=180°,
∴∠OBD=90°,
∴BD是⊙O的切线;
(2)延长CO交⊙O于点E,连接AE,过C作CH⊥AB于H.

①∵BD∥OC,∠D=30°,
∴∠ACE=∠D=30°,
∵CE为直径,
∴∠EAC=90°,
∴∠E=60°,
∴∠ABC=∠E=60°;
②∵OC=2,
∴CE=4,
∵∠EAC=90°,∠ACE=30°,
∴AE![]() CE=2,
CE=2,
∴AC![]() 2
2![]() .
.
∵∠BAC=45°,
∴AH=CH![]() AC
AC![]() 2
2![]() .
.
∵∠ABC=60°,
∴BH![]() CH
CH![]() ,
,
∴AB=AH+BH![]() .
.

练习册系列答案
相关题目