题目内容
【题目】已知:点O到△ABC的两边AB,AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在边BC上,OE⊥AB,OF⊥AC,垂足分别为E,F.求证:AB=AC;

(2)如图,若点O在△ABC的内部,求证:AB=AC;
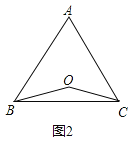
(3)若点O在△ABC的外部,AB=AC成立吗?请画出图表示.
【答案】(1)见解析;(2)见解析;(3)不一定成立,见解析.
【解析】
(1)求证AB=AC,就是求证∠B=∠C, 利用斜边直角边定理(HL)证明Rt△OEB≌Rt△OFC即可;
(2)首先得出Rt△OEB≌Rt△OFC,则∠OBE=∠OCF,由等边对等角得出∠OBC=∠OCB,进而得出∠ABC=∠ACB,由等角对等边即可得AB=AC;
(3)不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC.
(1)证明: ∵点O在边BC上,OE⊥AB,OF⊥AC,点O到△ABC的两边AB,AC所在直线的距离相等,
∴OE=OF,
在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠ABC=∠ACB,
∴AB=AC;
(2)证明:过点O分别作OE⊥AB于E,OF⊥AC于F,
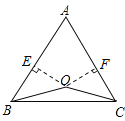
由题意知,OE=OF.∠BEO=∠CFO=90°,
∵在Rt△OEB和Rt△OFC中
![]()
∴Rt△OEB≌Rt△OFC(HL),
∴∠OBE=∠OCF,
又∵OB=OC,
∴∠OBC=∠OCB,
∴∠ABC=∠ACB,
∴AB=AC;
(3)解:不一定成立,当∠A的平分线所在直线与边BC的垂直平分线重合时AB=AC,否则AB≠AC.(如示例图)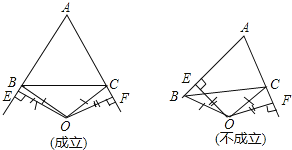

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目