题目内容
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙O经过点D,E是⊙O
上一点,且∠AED=45°。
(1)判断CD与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6cm,AE=10cm,求∠ADE的正弦值。
【答案】(1)CD与⊙O相切,理由见解析(2)![]()
【解析】
解:(1)连接BD,OD,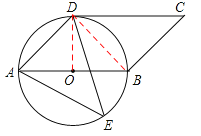
∵AB是直径,∴∠ADB=90°。
∵∠ABD=∠E=45°,∴∠DAB=45°,则AD=BD。
∴△ABD是等腰直角三角形。∴OD⊥AB。
又∵DC∥AB,∴OD⊥DC, ∴CD与⊙O相切。
(2)过点O作OF⊥AE,连接OE,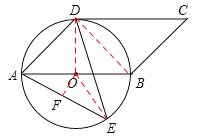
则AF=![]() AE=
AE=![]() ×10=5。
×10=5。
∵OA=OE,∴∠AOF=![]() ∠AOE。
∠AOE。
∵∠ADE=![]() ∠AOE,∴∠ADE=∠AOF。
∠AOE,∴∠ADE=∠AOF。
在Rt△AOF中,sin∠AOF=![]() ,
,
∴sin∠ADE= sin∠AOF =![]() 。
。
(1)连接OD,BD,由AB为直径,∠AED=45°,证得△ABD是等腰直角三角形,即AD=BD,
然后由等腰三角形的性质,可得OD⊥AB,又由四边形ABCD是平行四边形,即可证得OD⊥CD,即可
证得CD与⊙O相切。
(2)过点O作OF⊥AE,连接OE,由垂径定理可得AF=6,∠AOF=![]() ∠AOE,又由圆周角定理
∠AOE,又由圆周角定理
可得∠ADE=![]() ∠AOE,从而证得∠AOF=∠ADE,然后在Rt△AOF中,求得sin∠AOF的值,即可求得
∠AOE,从而证得∠AOF=∠ADE,然后在Rt△AOF中,求得sin∠AOF的值,即可求得
答案。

练习册系列答案
相关题目