题目内容
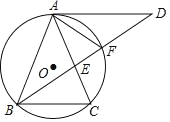
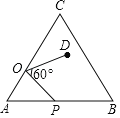
【题目】如图,在等边△ABC中,AC=9,点O在AC上,且AO=3,点P是AB上一动点,连结OP,将线段OP绕点O逆时针旋转60°得到线段OD,要使点D恰好落在BC上,则AP的长是( )
A.3B.5C.6D.8
【答案】C
【解析】
根据∠1+∠2=120°,∠1+∠3=120°,可得∠2=∠3,进而可以证明△AOP≌△CDO,进而可以证明AP=CO,即可解题.
解:如图,
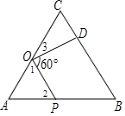
∵AC=9,AO=3,
∴OC=6,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵线段OP绕点D逆时针旋转60゜得到线段OD,要使点D恰好落在BC上,
∴OD=OP,∠POD=60°,
∵∠1+∠2+∠A=180°,∠1+∠3+∠POD=180°,
∴∠1+∠2=120°,∠1+∠3=120°,
∴∠2=∠3,
在△AOP和△CDO中,
∵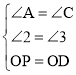 ,
,
∴△AOP≌△CDO,
∴AP=CO=6,
故选:C.

练习册系列答案
相关题目
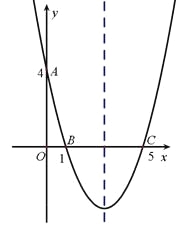
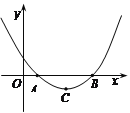
【题目】二次函数![]() (
(![]() ,
,![]() ,
,![]() 为常数,且
为常数,且![]() )中的
)中的![]() 与
与![]() 的部分对应值如下表:
的部分对应值如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
以下结论:
①二次函数![]() 有最小值为
有最小值为![]() ;
;
②当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
③二次函数![]() 的图象与
的图象与![]() 轴只有一个交点;
轴只有一个交点;
④当![]() 时,
时,![]() .
.
其中正确的结论有( )个
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()