题目内容
【题目】有A、B、C1、C2四张同样规格的硬纸片，它们的背面完全一样，正面如图1所示．将它们背面朝上洗匀后，随机抽取并拼图．
(1)填空：随机抽出一张，正面图形正好是中心对称图形的概率是__________．
(2)随机抽出两张(不放回)，其图形可拼成如图2的四种图案之一．请你用画树状图或列表的方法，分析拼成哪种图案的概率最大？
【答案】(1)
；（2）拼成电灯或房子的概率最大．
【解析】
（1）根据中心对称图形的定义得出四种图案哪些是中心对称图形，即可得出答案；
（2）首先根据题意画出树状图，然后根据树状图求得所有等可能的结果与拼成各种图案的情况，再利用概率公式即可求得答案．
解：（1）∵根据中心对称图形的性质，旋转180°后，能够与原图形完全重合的图形是中心对称图形，
∴只有A和B中图案符合，
∴正面图形正好是中心对称图形的概率=
；
（2）解：画树状图如下：
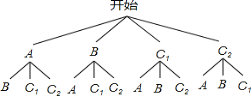
共有12种等可能的结果，拼成卡通人、电灯、房子、小山的分别有2，4，4，2种情况，
∴P(卡通人)=
=
，P(电灯)=
=
，P(房子)==，P(小山)==，
∴拼成电灯或房子的概率最大．
练习册系列答案
相关题目
