题目内容
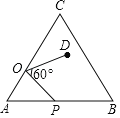
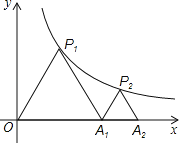
【题目】如图,P1是反比例函数![]() (k>0)在第一象限图象上的一点,点A1的坐标为(2,0).若△P1OA1与△P2A1A2均为等边三角形,则A2点的坐标为_____.
(k>0)在第一象限图象上的一点,点A1的坐标为(2,0).若△P1OA1与△P2A1A2均为等边三角形,则A2点的坐标为_____.
【答案】(2![]() ,0)
,0)
【解析】
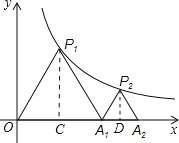
由于△P1OA1为等边三角形,作P1C⊥OA1,垂足为C,由等边三角形的性质及勾股定理可求出点P1的坐标,根据点P1是反比例函数y=![]() (k>0)图象上的一点,利用待定系数法求出此反比例函数的解析式;作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
(k>0)图象上的一点,利用待定系数法求出此反比例函数的解析式;作P2D⊥A1A2,垂足为D.设A1D=a,由于△P2A1A2为等边三角形,由等边三角形的性质及勾股定理,可用含a的代数式分别表示点P2的横、纵坐标,再代入反比例函数的解析式中,求出a的值,进而得出A2点的坐标.
作P1C⊥OA1,垂足为C,
∵△P1OA1为边长是2的等边三角形,
∴OC=1,P1C=2×![]() =
=![]() ,
,
∴P1(1,![]() ).
).
代入y=![]() ,得k=
,得k=![]() ,
,
所以反比例函数的解析式为y=![]() .
.
作P2D⊥A1A2,垂足为D.
设A1D=a,
则OD=2+a,P2D=![]() a,
a,
∴P2(2+a,![]() a).
a).
∵P2(2+a,![]() a)在反比例函数的图象上,
a)在反比例函数的图象上,
∴代入y=![]() ,得(2+a)
,得(2+a)![]() a=
a=![]() ,
,
化简得a2+2a﹣1=0
解得:a=﹣1±![]() .
.
∵a>0,
∴a=﹣1+![]() .∴A1A2=﹣2+2
.∴A1A2=﹣2+2![]() ,
,
∴OA2=OA1+A1A2=2![]() ,
,
所以点A2的坐标为(2![]() ,0).
,0).
故答案为:(2![]() ,0).
,0).

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目