Question

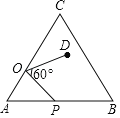
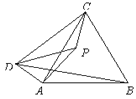
【题目】如图，P为等边△ABC内一点，∠APC=150°，且∠APD=30°，AP=6，CP=3，DP=7，则BD的长为______.

Answer 1

【答案】2.

【解析】

将△CPA绕点C逆时针旋转60°得到△CEB，连接EP，由全等三角形的性质可得CE=CP，∠ECB=∠PCA，∠CEB=∠CPA=150°，BE=AP=6，结合等边三角形的性质可得出∠ECP=60°，进而证明△ECP为等边三角形，由等边△ECP的性质进而证明D、P、E三点共线以及∠DEB=90°，最后利用勾股定理求出BD的长度即可.

将△CPA绕点C逆时针旋转60°得到△CEB，连接EP，

∴CE=CP，∠ECB=∠PCA，∠CEB=∠CPA=150°，BE=AP=6，

∵等边△ABC，

∴∠ACP+∠PCB=60°，

∴∠ECB+∠PCB=60°,即∠ECP=60°，

∴△ECP为等边三角形，

∴∠CPE=∠CEP=60°，PE=6，

∴∠DEB=90°，

∵∠APC=150°，∠APD=30°，

∴∠DPC=120°，

∴∠DPE=180°，即D、P、E三点共线，

∴ED=3+7=10，

∴BD==2.

故答案为2.