Question

【题目】在平面直角坐标系xoy中，对于某点P（P不是原点），称以点P为圆心，长为半径圆为点P的半长圆；对于点Q，若将点P的半长圆绕原点旋转，能够使得点Q位于点P的半长圆内部或圆上，则称点Q能被点P半长捕获（或点P能半长捕获点Q）．

（1）在平面直角坐标系xoy中，点M（2，0），则点M的半长圆的面积为 ；下列各点，能被点M半长捕获的点有 ；

（2）已知点，

①点N（0，n），当t=1时，线段EF上的所有点均可以被点N半长捕获，求n的取值范围；

②若对于平面上的任意点（原点除外）都不能半长捕获线段EF上的所有点，直接写出t的取值范围．

Answer 1

【答案】（1），B点和C点；（2）①或；②．

【解析】

（1）根据M点坐标，先求出M的半长圆的半径，由此可求面积，再根据题述定义，画出大致图，由图可知被点M半长捕获的点到原点的距离介于1到3之间，分别计算出各点到圆心的距离，即可得出被点M半长捕获的点；

（2）①当n＞0时，根据题述定义可得被点N半长捕获的点到原点的距离介于到之间，由此可列出不等式组，即可求得n的取值范围，同理可求得n＜0时，n的取值范围；

②设半长圆的半径为r，则被点N半长捕获的点到原点的距离介于r到3r之间，根据题意，可列出关于r的不等式组，且该不等式组无解，即可求得t的取值范围．

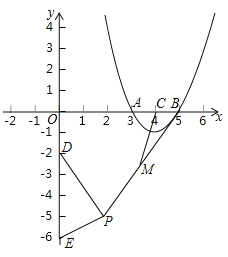
解：（1）如下图，

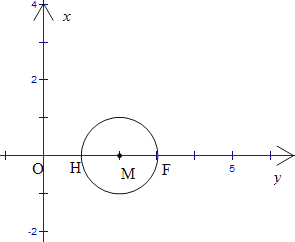
∵M（2，0）,

∴过M点的半长圆半径为1，即HM=MF=1,

∴OH=1,OF=3，,

∴被点M半长捕获的点到原点的距离介于1到3之间，

又∵,

∴,

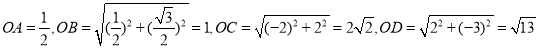所以，能被点M半长捕获的点有B点和C点．

故答案为：，B点和C点；

（2）①根据点N（0，n），

若n＞0，则半长圆的半径为，

此时，被点N半长捕获的点到原点的距离介于到之间，

∵且，

∴,

又∵线段EF上的所有点均可以被点N半长捕获，

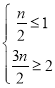∴，解得，

若n＜0，同理可得，

故或；

②∵，

∴，

设半长圆的半径为r，

则被点N半长捕获的点到原点的距离介于r到3r之间，

若对于平面上的任意点（原点除外）都不能半长捕获线段EF上的所有点，则

关于r的不等式组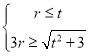 无解，

即，解得，

又∵，

∴，