题目内容
如图,平面直角坐标系中有一矩形ABCD(O为原点),点A、C分别在x轴、y轴上,且C点坐标为(0,6);将BCD沿BD折叠(D点在OC边上),使C点落在OA边的E点上,并将BAE沿BE折叠,恰好使点A落在BD的点F上.
(1)直接写出∠ABE、∠CBD的度数,并求折痕BD所在直线的函数解析式;
(2)过F点作FG⊥x轴,垂足为G,FG的中点为H,若抛物线![]() 经过B、H、D三点,求抛物线的函数解析式;
经过B、H、D三点,求抛物线的函数解析式;
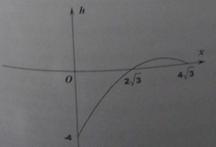
(3)若点P是矩形内部的点,且点P在(2)中的抛物线上运动(不含B、D点),过点P作PN⊥BC分别交BC和BD于点N、M,设h=PM-MN,试求出h与P点横坐标x的函数解析式,并画出该函数的简图,分别写出使PM<NM、PM=MN、PM>MN成立的x的取值范围。
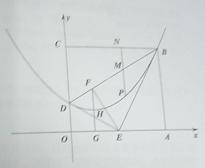
解:(1)∠ABE=∠CBD=30°
在△ABE中,AB=6
BC=BE=![]()
CD=BCtan30°=4
∴OD=OC-CD=2
∴B(![]() ,6) D(0,2)
,6) D(0,2)
设BD所在直线的函数解析式是y=kx+b
![]()
![]()
![]() ∴
∴ 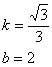
所以BD所在直线的函数解析式是![]()
(2)∵EF=EA=ABtan30°=![]() ∠FEG=180°-∠FEB-∠AEB=60°
∠FEG=180°-∠FEB-∠AEB=60°
又∵FG⊥OA
∴FG=EFsin60°=3 GE=EFcos60°=![]() OG=OA-AE-GE=
OG=OA-AE-GE=![]()
又H为FG中点
∴H(![]() ,
,![]() )
)
∵B(![]() ,6) 、 D(0,2)、 H(
,6) 、 D(0,2)、 H(![]() ,
,![]() )在抛物线
)在抛物线![]() 图象上
图象上
![]()
![]()
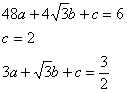 ∴
∴ 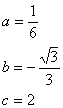
∴抛物线的解析式是![]()
(2)∵MP=![]()
MN=6-![]()
H=MP-MN=![]()
由![]() 得
得![]()
该函数简图如图所示:
当0<x<![]() 时,h<0,即HP<MN
时,h<0,即HP<MN
当x=![]() 时,h=0,即HP=MN
时,h=0,即HP=MN
当![]() <x<
<x<![]() 时,h>0,即HP>MN
时,h>0,即HP>MN

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线
如图,平面直角坐标系中,O为直角三角形ABC的直角顶点,∠B=30°,锐角顶点A在双曲线 =2
=2 如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
如图,平面直角坐标系中,OB在x轴上,∠ABO=90°,点A的坐标为(1,2).将△AOB绕点A逆时针旋转90°,则点O的对应点C的坐标为( )
 如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.
如图在平面直角坐标系中,A点坐标为(8,0),B点坐标为(0,6)C是线段AB的中点.请问在y轴上是否存在一点P,使得以P、B、C为顶点的三角形与△AOB相似?若存在,求出P点坐标;若不存在,说明理由.