题目内容
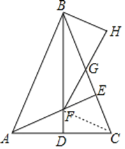
【题目】如图,在△ABC中,AB=BC,∠ABC=45°,点D是AC的中点,连接BD,作AE⊥BC于E,交BD于点F,点G是BC的中点,连接FG,过点B作BH⊥AB交FG的延长线于H.
(1)若AB=3![]() ,求AF的长;
,求AF的长;
(2)求证;BH+2CE=AB.

【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】
(1)由条件得△ABE是等腰直角三角形,AE=3,可证△AEC≌△BEF,有EF=CE,根据等腰三角形的性质可知BD是AC的中垂线,连结CF,则AF=CF,设AF=x,EF=3-x,在Rt△EFC中,(3-x)2+(3-x)2=x2,解此方程即可;
(2)可先证△BGH≌△CGF,可得BH=CF=AF,由AE=BE=AF+EF,BE+CE=BC=AB,即可得证.
(1)连结CF,
∵AE⊥BC,∠ABC=45°,
∴AE=BE,AE=ABsin45°=![]() ,
,
∵AB=BC,点D是AC的中点,
∴∠ADB=∠BDC=90°,
∴AF=CF,∠CAE=∠DBC,
在△AEC和△BEF中,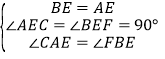 ,
,
∴△AEC≌△BEF (AAS),
∴CE=EF,
设AF=x,EF=3-x,在Rt△EFC中,CE2+EF2=CF2,
∴(3-x)2+(3-x)2=x2,解得,x=![]() ,
,
(2)证明:∵BH⊥AB,∠ABC=45°,
∴∠HBG=45°,
由(1)知∠FCE=45°,
∴∠FCE=∠HBG,
∵点G是BC的中点,
∴BG=CG,
在△BGH和△CGF中,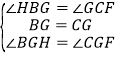 ,
,
∴△BGH≌△CGF(ASA),
∴BH=CF,
∴AB=BE+CE=AE+CE=AF+EF+CE,
∴AB=BH+CE+CE=BH+2CE.

【题目】七年级320名学生参加安全知识竞赛活动,小明随机调查了部分学生的成绩(分数为整数),绘制了频率分布表和频数分布直方图(不完整),请结合图表信息回答下列问题:
成绩(分) | 频数 |
71≤x<76 | 2 |
76≤x<81 | 8 |
81≤x<86 | 12 |
86≤x<91 | 10 |
91≤x<96 | 6 |
96≤x<101 | 2 |

(1)补全频数直方图;
(2)小明调查的学生人数是_______;频率分布表的组距是_______;
(3)七年级参加本次竞赛活动,分数![]() 在
在![]() 范围内的学生约有多少人.
范围内的学生约有多少人.





