题目内容
【题目】如图,边长为a的等边△ACB中,E是对称轴AD上一个动点,连EC,将线段EC绕点C逆时针旋转60°得到MC,连DM,则在点E运动过程中,DM的最小值是。
【答案】1.5
【解析】解:如图,取AC的中点G,连接EG, 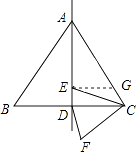
∵旋转角为60°,
∴∠ECD+∠DCF=60°,
又∵∠ECD+∠GCE=∠ACB=60°,
∴∠DCF=∠GCE,
∵AD是等边△ABC的对称轴,
∴CD= ![]() BC,
BC,
∴CD=CG,
又∵CE旋转到CF,
∴CE=CF,
在△DCF和△GCE中,
 ,
,
∴△DCF≌△GCE(SAS),
∴DF=EG,
根据垂线段最短,EG⊥AD时,EG最短,即DF最短,
此时∵∠CAD= ![]() ×60°=30°,AG=
×60°=30°,AG= ![]() AC=
AC= ![]() ×6=3,
×6=3,
∴EG= ![]() AG=
AG= ![]() ×3=1.5,
×3=1.5,
∴DF=1.5.
所以答案是:1.5.
【考点精析】利用垂线段最短和等边三角形的性质对题目进行判断即可得到答案,需要熟知连接直线外一点与直线上各点的所有线段中,垂线段最短;现实生活中开沟引水,牵牛喝水都是“垂线段最短”性质的应用;等边三角形的三个角都相等并且每个角都是60°.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目






