题目内容
在△ABC中,∠C=60°.两条角平分线AD,BE所在直线所成的角的度数是( )
| A.60° | B.120° | C.150° | D.60°或120° |
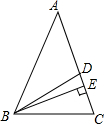
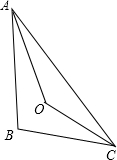
当AD与BE是△ABC内角平分线时,如图1所示:
在△ABC中,∵∠C=60°,
∴∠CAB+∠ABC=180°-60°=120°,
∵AD,BE分别是∠CAB与∠ABC的平分线,
∴∠OAB+∠OBA=
(∠CAB+∠ABC)=
×120°=60°,
∴∠AOB=180°-(∠OAB+∠OBA)=180°-60°=120°;
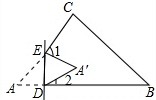
当当AD与BE是△ABC外角平分线时,如图2所示:
在△ABC中,∵∠C=60°,
∴∠CAB+∠ABC=180°-60°=120°,
∴∠FAB+∠GBA=360°-(∠CAB+∠ABC)=360°-120°=240°,
∵AD,BE分别是∠FAB与∠GBA的平分线,
∴∠OAB+∠OBA=
(∠FAB+∠GBA)=
×240°=120°,
∴∠AOB=180°-(∠OAB+∠OBA)=180°-120°=60°.
故选D.
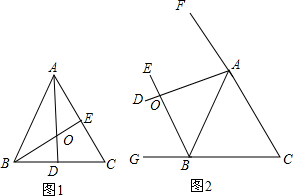
在△ABC中,∵∠C=60°,
∴∠CAB+∠ABC=180°-60°=120°,
∵AD,BE分别是∠CAB与∠ABC的平分线,
∴∠OAB+∠OBA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOB=180°-(∠OAB+∠OBA)=180°-60°=120°;
当当AD与BE是△ABC外角平分线时,如图2所示:
在△ABC中,∵∠C=60°,
∴∠CAB+∠ABC=180°-60°=120°,
∴∠FAB+∠GBA=360°-(∠CAB+∠ABC)=360°-120°=240°,
∵AD,BE分别是∠FAB与∠GBA的平分线,
∴∠OAB+∠OBA=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠AOB=180°-(∠OAB+∠OBA)=180°-120°=60°.
故选D.


练习册系列答案
相关题目