题目内容
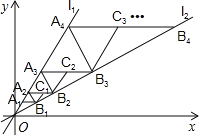
【题目】如图,点A1在直线l1:y=![]() x上,过点A1作x轴的平行线交直线l2:y=
x上,过点A1作x轴的平行线交直线l2:y=![]() x于点B1,
x于点B1,
过点B1作l2的垂线交l1于点A2,过点A2作x轴的平行线交直线l2于点B2,过点B2作l2的垂线交l1于点A3,过点A3作x轴的平行线交直线l2于点B3,……,过点B1,B2,B3,……,分别作l1的平行线交A2B2于点C1,交A3B3于点C2,交A4B4于点C3,……,按此规律继续下去,若OA1=1,则点![]() 的坐标为_______________.
的坐标为_______________.
【答案】![]()
【解析】
根据两直线的解析式分别求![]() 与
与![]() 的坐标坐标,求出
的坐标坐标,求出![]() 等线段的长,然后根据四边形
等线段的长,然后根据四边形![]() 是菱形求解进而代入
是菱形求解进而代入![]() 计算即可.
计算即可.
解:∵![]() ,
,
∴l1与x轴的夹角为60°,
∵![]() ,
,
∴l2与x轴的夹角为30°,
∵点B1作l2的垂线交l1于点A2,
∴![]() 是等边三角形,
是等边三角形,
同理可得![]() 等边三角形
等边三角形
∴四边形![]() 是菱形;
是菱形;
∵OA1=1,
∴点A1的坐标为:![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴点B1的横坐标为![]() ,
,
∴点A2的横坐标为: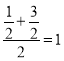 ,
,
∴OA2=2,
∴![]() ,
,
∴![]() ,
,
∴点A2的纵坐标为![]() ,
,
∴点C1的横坐标为:2,
即点C1的坐标为(21,![]() );
);
∴点A3的横坐标为2,
∴点C2的横坐标为:2+2=4,
∵点A3的纵坐标为2![]()
∴点C2的横坐标为:2![]() ,
,
故点C2的坐标为(22,21![]() ),
),
…
则点Cn的坐标为(2n,![]() ).
).
当![]() 时,则有
时,则有![]() 为
为![]()
故答案为:![]() .
.

练习册系列答案
相关题目