题目内容
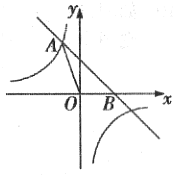
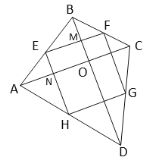
【题目】四边形ABCD中,对角线AC、BD相互垂直,AC=4,BD=6,顺次联结这个四边形中点所得的四边形的面积等于________
【答案】6
【解析】
根据E、F、G、H分别为各边的中点,得到EF∥AC,GH∥AC,EH∥BD,FG∥BD,EF=![]() AC=2,EH=
AC=2,EH=![]() BD=3,证得四边形EFGH是平行四边形,根据AC⊥BD,EF∥AC,EH∥BD,求出∠EMO=∠ENO=90°,证得四边形EMON是矩形,得到∠MEN=90°,由此证得四边形EFGH是矩形,再利用面积公式计算即可.
BD=3,证得四边形EFGH是平行四边形,根据AC⊥BD,EF∥AC,EH∥BD,求出∠EMO=∠ENO=90°,证得四边形EMON是矩形,得到∠MEN=90°,由此证得四边形EFGH是矩形,再利用面积公式计算即可.
如图:
∵E、F、G、H分别为各边的中点,
∴EF∥AC,GH∥AC,EH∥BD,FG∥BD,EF=![]() AC=2,EH=
AC=2,EH=![]() BD=3,
BD=3,
∴四边形EFGH是平行四边形,
∵AC⊥BD,EF∥AC,EH∥BD,
∴∠EMO=∠ENO=90°,
∴四边形EMON是矩形,
∴∠MEN=90°,
∴四边形EFGH是矩形,
∴四边形EFGH的面积=![]() ,
,
故答案为:6.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案
相关题目
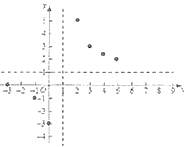
【题目】有这样一个问题:探究函数![]() 的图象与性质,小李根据学习函数的经验,对函数
的图象与性质,小李根据学习函数的经验,对函数![]() 的图象与性质进行了探究.
的图象与性质进行了探究.
下面是小李探究的过程,请补充完整:
(1)函数![]() 的自变量
的自变量![]() 的取值范围是______;
的取值范围是______;
(2)下表是![]() 与
与![]() 的几组对应值:
的几组对应值:
| … |
|
|
| 0 | 2 | 3 | 4 | 5 | … |
| … | 0 |
|
|
| 5 | 3 |
| 2 | … |
则![]() 的值为_______;
的值为_______;
(3)如图所示,在平面直角坐标系![]() 中,根据描出的点,请补全此函数的图象;
中,根据描出的点,请补全此函数的图象;
(4)观察图象,写出该函数的一条性质_______;
(5)若函数![]() 的图象在函数
的图象在函数![]() 的图象上方,直接写出
的图象上方,直接写出![]() 的取值范围_______.
的取值范围_______.