题目内容
【题目】如图,在平面直角坐标系中,A(﹣1,5),B(﹣1,0),C(﹣4,3).

(1)请画出△ABC关于y轴对称的△DEF(其中D,E,F分别是A,B,C的对应点,不写画法);
(2)直接写出D,E,F三点的坐标:D( ),E( ),F( );
(3)在y轴上存在一点,使PC﹣PB最大,则点P的坐标为 .
【答案】(1)如图,△DEF即为所求作三角形;见解析;(2)点D(1,5)、E(1,0)、F(4,3);(3)点P坐标为(0,﹣1),
【解析】
(1)分别作出点A、B、C关于y轴对称点D、E、F,即可得△DEF;
(2)根据(1)中图形可得坐标;
(3)延长CB交y轴于P,点P即为所求,待定系数法求直线BC所在直线解析式,即可知其与y轴的交点P的坐标.
(1)如图,△DEF即为所求作三角形;
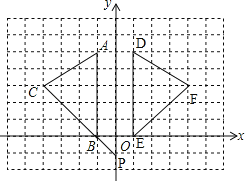
(2)由图可知点D(1,5)、E(1,0)、F(4,3),
故答案为:1,5;1,0;4,3;
(3)延长CB交y轴于P,此时PC﹣PB最大,故点P即为所求,
设BC所在直线解析式为y=kx+b,
将点B(﹣1,0)、点C(﹣4,3)代入,得:![]() ,
,
解得:![]() ,
,
∴直线BC所在直线解析式为y=﹣x﹣1,
当x=0时,y=﹣1,
∴点P坐标为(0,﹣1),
故答案为:(0,﹣1).

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
【题目】某校从两名优秀选手中选一名参加全市中小学运动会的男子![]() 米跑项目,该校预先对这两名选手测试了
米跑项目,该校预先对这两名选手测试了![]() 次,测试成绩如下表
次,测试成绩如下表
|
|
|
|
|
|
|
| |
甲的成绩(秒) |
|
|
|
|
|
|
|
|
乙的成绩(秒) |
|
|
|
|
|
|
|
|
![]() 为了衡量这两名选手
为了衡量这两名选手![]() 米跑的水平,你选择哪些统计量?请分别求出这些统计量的值.
米跑的水平,你选择哪些统计量?请分别求出这些统计量的值.
![]() 你认为选派谁比较合适?为什么?
你认为选派谁比较合适?为什么?