题目内容
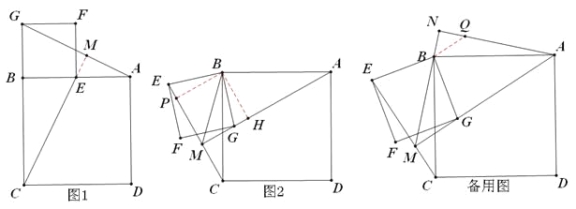
【题目】如图,四边形ABCD、BEFG均为正方形,
(1)如图1,连接AG、CE,试判断AG和CE的数量和位置关系并证明.
(2)将正方形BEFG绕点B顺时针旋转β角(0°<β<180°),如图2,连接AG、CE相交于点M,连接MB,当角β发生变化时,∠EMB的度数是否发生变化?若不变化,求出∠EMB的度数;若发生变化,请说明理由.
(3)在(2)的条件下,过点A作AN⊥MB交MB的延长线于点N,请直接写出线段CM与BN的数量关系.

【答案】详见解析.
【解析】试题分析:
(1)判断![]() 和
和![]() 的数量关系,可通过
的数量关系,可通过![]() 证
证![]() 求解.判断
求解.判断![]() 和
和![]() 的位置关系,可延长
的位置关系,可延长![]() 交
交![]() 于点
于点![]() ,求
,求![]() 即可。
即可。
(2)![]() ,理由是:过点
,理由是:过点![]() 作
作![]() ,
,![]() ,利用
,利用![]() 得出
得出![]() ,由全等三角形得到面积相等,而
,由全等三角形得到面积相等,而![]() ,可得出
,可得出![]() ,由到角两边距离相等的点在角的平分线上得
,由到角两边距离相等的点在角的平分线上得![]() 为
为![]() 的角平分线,再由
的角平分线,再由![]() ,及一对对顶角相等,可得
,及一对对顶角相等,可得![]() ,利用角平分线的定义即可求解.
,利用角平分线的定义即可求解.
(3)![]() .如备用图,在
.如备用图,在![]() 上截取
上截取![]() ,由
,由![]() 可得
可得![]() 为等腰直角三角形,由勾股定理得
为等腰直角三角形,由勾股定理得![]() ,然后证
,然后证![]() ,因为
,因为![]() (理由:
(理由:![]() ;由问题2中
;由问题2中![]() 得
得![]() ;以及正方形的边
;以及正方形的边![]() .由
.由![]() 可得全等).根据全等三角形的对应边相等即可求证.
可得全等).根据全等三角形的对应边相等即可求证.
试题解析:
解:(1)![]() ,
,![]() 理由如下:如上图1,
理由如下:如上图1,
∵四边形BEFG和ABCD为正方形
∴![]()
![]()
![]()
![]()
∵在![]() 和
和![]() 中
中
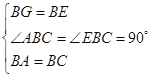
∴![]()
∴![]() ,
,![]()
延长![]() 交
交![]() 于点
于点![]() ,
,
∴![]()
∴![]()
∴![]()
(2)![]() ,理由如下:如上图2
,理由如下:如上图2
过点![]() 作
作![]() ,
,![]()
在![]() 和
和![]() 中
中
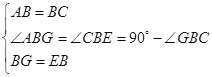
∴![]()
∴![]()
∴![]()
∴![]()
∴![]() 平分
平分![]()
∵![]()
∴![]()
(3)![]()

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目



